Методом математической индукции докажите справедливость неравенства!
Приложения:
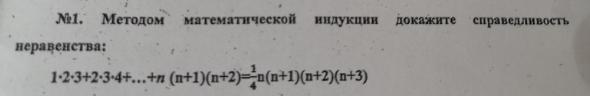
Аноним:
Здесь не неравенство, а равенство
Ответы
Ответ дал:
0
Ответ: Доказательство ниже.
Пошаговое объяснение:
База:
n=1:
1*2*3=0,25*1*2*3*4=1*2*3 - верно.
Пусть для n=k это равенство верно.
Докажем для n=k+1:
1*2*3+2*3*4+...+k(k+1)(k+2)+(k+1)(k+2)(k+3)=0,25(k+1)(k+2)(k+3)(k+4)
Перенесём (k+1)(k+2)(k+3) направо:
1*2*3+2*3*4+...+k(k+1)(k+2)=0,25(k+1)(k+2)(k+3)(k+4)-(k+1)(k+2)(k+3)=(k+1)(k+2)(k+3)(0,25k+1-1)=0,25k(k+1)(k+2)(k+3), но 1*2*3+2*3*4+...+k(k+1)(k+2)=0,25k(k+1)(k+2)(k+3), значит для n=k+1 равенство доказано.
Причем тут k?
Вас заинтересует
1 год назад
1 год назад
1 год назад
3 года назад
3 года назад
8 лет назад