В равнобедренный треугольник ABC вписана окружность с радиусом 5. Вторая окружность с радиусом 2 касается равных сторон треугольника, а также первой окружности внешним образом. Найдите радиус описанной окружности треугольника ABC.
Simba2017:
времени сколько есть
где-то 45 минут
высота треугольника этого 16 2.3
16 2/3
все находится
долго выводить, да и радиус нецелый.. ошибка в вычислениях наверное
каких равных сторон - имеется ввиду боковую сторону?
около 10 ответ
Ответы
Ответ дал:
0
..............................................
Приложения:
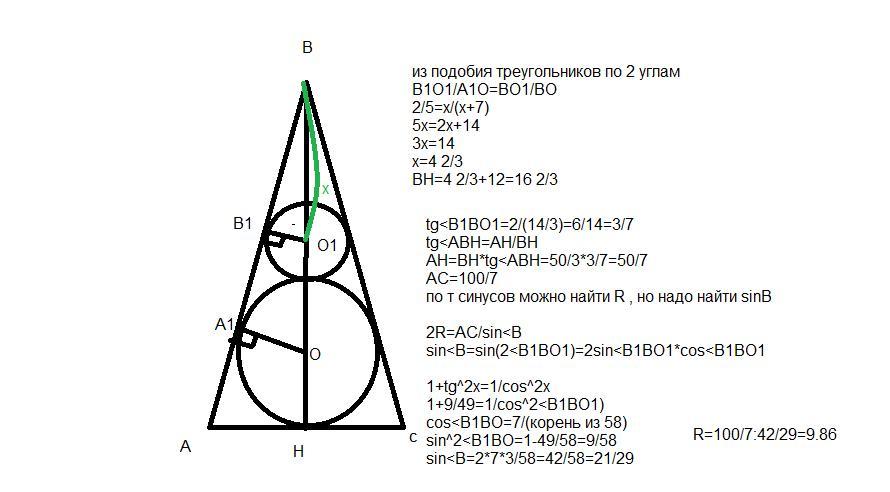
R= 245/24
I - центр вписанной окружности, N - точка касания окружностей. 2R= BI^2/BN
а поподробнее
Нашли x=14/3; BH=50/3; B/2=ф
sinф =2/x =3/7; cosф =2V10/7
cosф =BH/AB; cosф =AB/2R
R =BH/2cosф^2 =50/3 : 2*40/49
sinф =2/x =3/7; cosф =2V10/7
cosф =BH/AB; cosф =AB/2R
R =BH/2cosф^2 =50/3 : 2*40/49
Ответ дал:
1
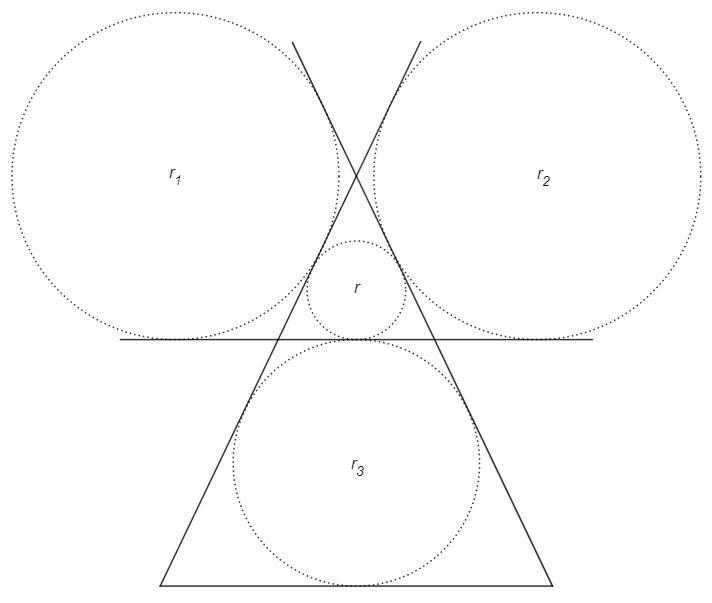
Проведем общую касательную через точку касания окружностей. Рассмотрим треугольник, в который вписана меньшая окружность (r), и его вневписанные окружности (r₁, r₂, r₃). Найдем его описанную окружность (R).
r₁=r₂, r₃=5, r=2
1/r = 1/r₁ + 1/r₂ + 1/r₃
1/2 = 1/r₁ +1/r₁ +1/5 => r₁=20/3
4R = r₁ + r₂ + r₃ - r
4R = 20/3 +20/3 +5 -2 => R=49/12
R₃ - искомая описанная окружность.
R₃/R =5/2 => R₃= 49/12 *5/2 =245/24
Приложения:
R-тогда что?
нашла я эту теорему и выходит что R-это радиус описанной окружности малого треугольника. Из подобия треугольников следует подобие радиусов описанных окружностей тогда вероятно...
Вас заинтересует
1 год назад
1 год назад
1 год назад
1 год назад
3 года назад