Ответы
Ответ:
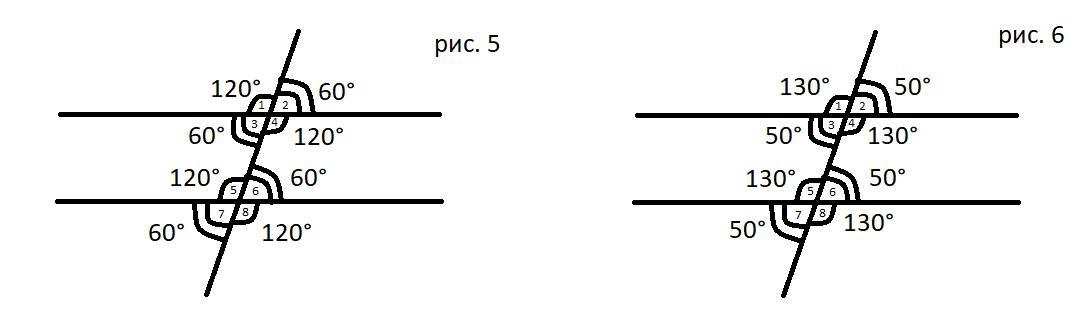
1) 120°, 60°; 60°; 120°, 120°, 60°, 60°, 120°.
2) 130°, 50°, 50°, 130°, 130°, 50°, 50°, 130°.
Объяснение:
№ 1.
Дано:
∠ 1 = 120°.
Найти:
∠ 2; ∠ 3; ∠ 4; ∠ 5; ∠ 6; ∠ 7; ∠ 8.
Решение:
Обозначим прямые буквами a и b, а секущую буквой с. Также прономеруем углы от 1 до 8. Теперь приступим к рассуждению.
∠ 1 = ∠ 8, а они накрест лежащие при прямых a и b и секущей c ⇒ ∠ 8 = 120°, а также по теореме a ║ b.
∠ 1 + ∠ 2 = 180°, т.к. они смежные ⇒ ∠ 2 = 180 - ∠ 1 = 180 - 120 = 60°.
∠ 8 = ∠ 5, т.к. они вертикальные ⇒ ∠ 5 = 120°.
∠ 5 + ∠ 6 = 180°, т.к. они смежные ⇒ ∠ 6 = 180 - ∠ 5 = 180 - 120 = 60°.
∠ 1 = ∠ 4, т.к. они вертикальные ⇒ ∠ 4 = 120°.
∠ 2 = ∠ 3, т.к. они вертикальные ⇒ ∠ 3 = 60°.
∠ 6 = ∠ 7, т.к. они вертикальные ⇒ ∠ 7 = 60°
№ 2.
Дано:
∠ 7 = 50°.
Найти:
∠ 1; ∠ 2; ∠ 3; ∠ 4; ∠ 5; ∠ 6; ∠ 8.
Решение:
Обозначим прямые буквами a и b, а секущую буквой с. Также прономеруем углы от 1 до 8. Теперь приступим к рассуждению.
∠ 7 = ∠ 2, а они накрест лежащие при прямых a и b и секущей c ⇒ ∠ 2 = 50°, а также по теореме a ║ b.
∠ 2 + ∠ 1 = 180°, т.к. они смежные ⇒ ∠ 1 = 180 - ∠ 2 = 180 - 50 = 130°.
∠ 2 = ∠ 3, т.к. они вертикальные ⇒ ∠ 3 = 50°.
∠ 2 = ∠ 6, т.к. они соответственные при a ║ b и секущей с ⇒ ∠ 6 = 50°.
∠ 6 + ∠ 5 = 180°, т.к. они смежные ⇒ ∠ 5 = 180 - ∠ 6 = 180 - 50 = 130°.
∠ 5 = ∠ 8, т.к. они вертикальные ⇒ ∠ 8 = 130°.
∠ 3 + ∠ 4 = 180°, т.к. они смежные ⇒ ∠ 4 = 180 - ∠ 3 = 180 - 50 = 130°.