Question

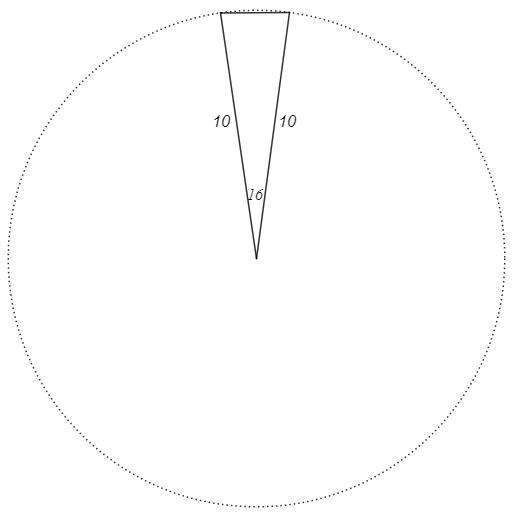
угол между двумя радиуеами окружности равеь16гдадусов. Найдите с точностью до 0,1ди длину хорды, соердиняющей концы этих радиусов, если диаметр окружности равен 10дм​

Answer 1

теорема косинусов

c^2 = a^2 +b^2 -2ab*cosC  

для равнобедренного треугольника

c= a√2 √(1-cosC)  

c= 10√2 √(1-cos16) =10√2 *0,1968  

~2,78 или ~2,8 (дм)

---------------------------------------

Если принять cos16 ~24/25

c= 10√2 *√(1 -24/25) =10√2/5 =2√2 (~2,8) (дм)