Question

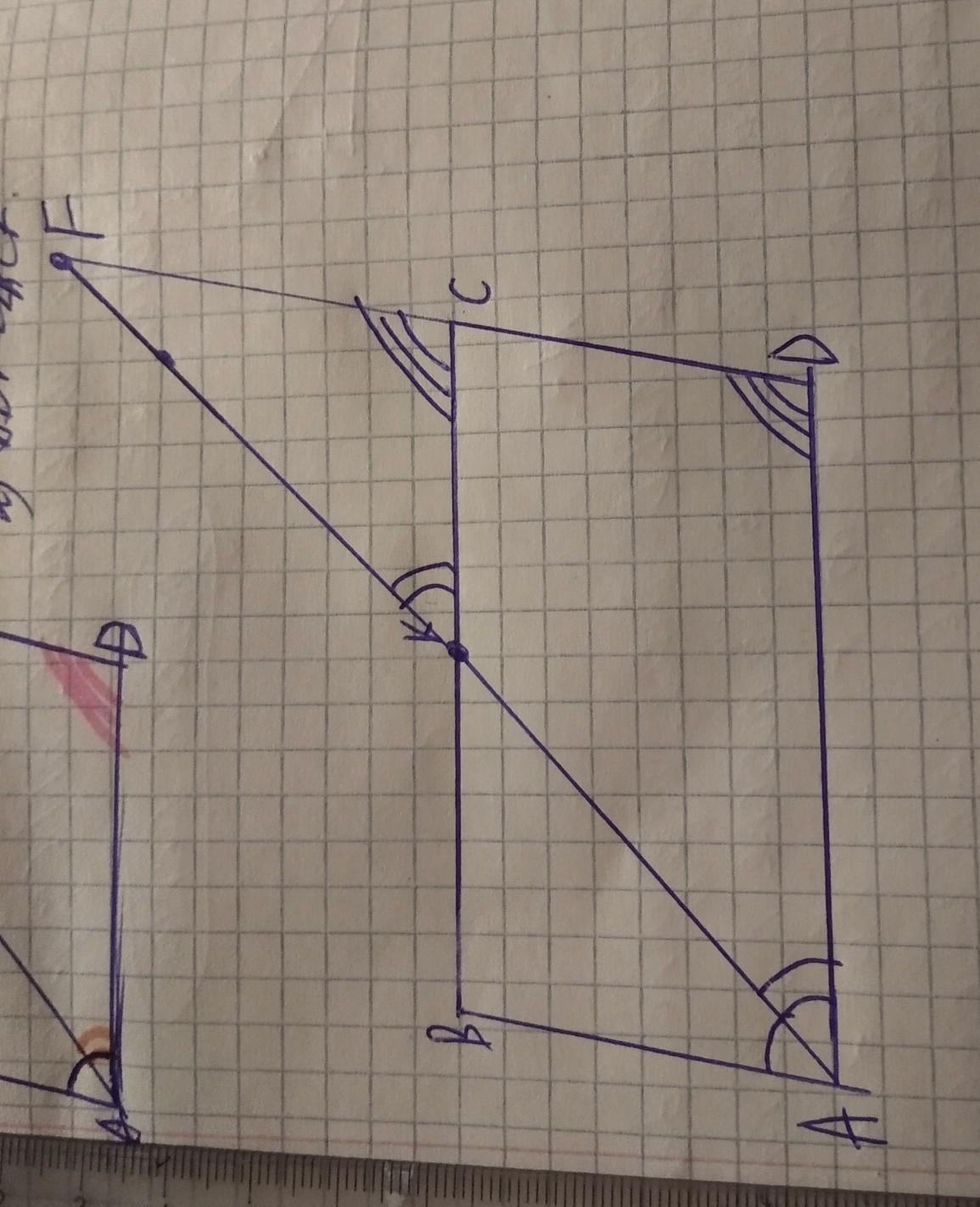
В параллелограмме АВСD биссектриса острого угла ВАD пересекает сторону ВС, в точке К, а продолжение стороны СD в точке F,
FC:FD=3:4
a) докажите, что треугольники KFC и AFD подобны??
б) Найдите стороны параллелограмма ABCD, если его Периметр = 32см
СРОЧНООО ПОЖАЛУЙСТА ПОМОГИТЕЕЕ
ПОЖАЛУЙСТА, ПОДРОБНОЕ РЕШЕНИЕ и Дано ....​

Answer 1

Ответ:

(на картинке)

Объяснение:

Answer 2

Ответ:

Объяснение:

а)Если два угла одного треугольника соответственно равны двум углам другого, то такие треугольники подобны.  

Δ KFC подобен Δ AFD т.к.  ∠FKC=∠KAD как соответственные при КС ║ АД и АF-секущая  ; ∠FCK=∠FDA при КС ║ АД и DF-секущая.

б) 1)Т.к. АД-биссектриса, то ∠ДАК=∠ВАК .

И ∠ДАК=∠ВКА как накрест лежащие при КВ ║ АД и АК-секущая. Поэтому Δ KАВ-равнобедренный и значит Ав=ВК.

2)Пусть АД=х, тогда ДС=16-х ( полупериметр 32:2=16).

АВ=СД=16-х  ,тогда ВК=16-х .

КС=ВС-ВК  ,КС=х-(16-х)=2х-16.

3)Δ KFC подобен Δ AFD, значит сходственные стороны пропорциональны :FC/FD=КС/АД  ,3/4=(2х-16)/х  ,3х=4*(2х-16)  ,

3х=8х-64  , -5х=-64  ,х=12,8  АД=12,8.

Тогда СД=16-12,8=3,2