Question

Помогите пожалуйста срочно!!! 60 баллов!!!
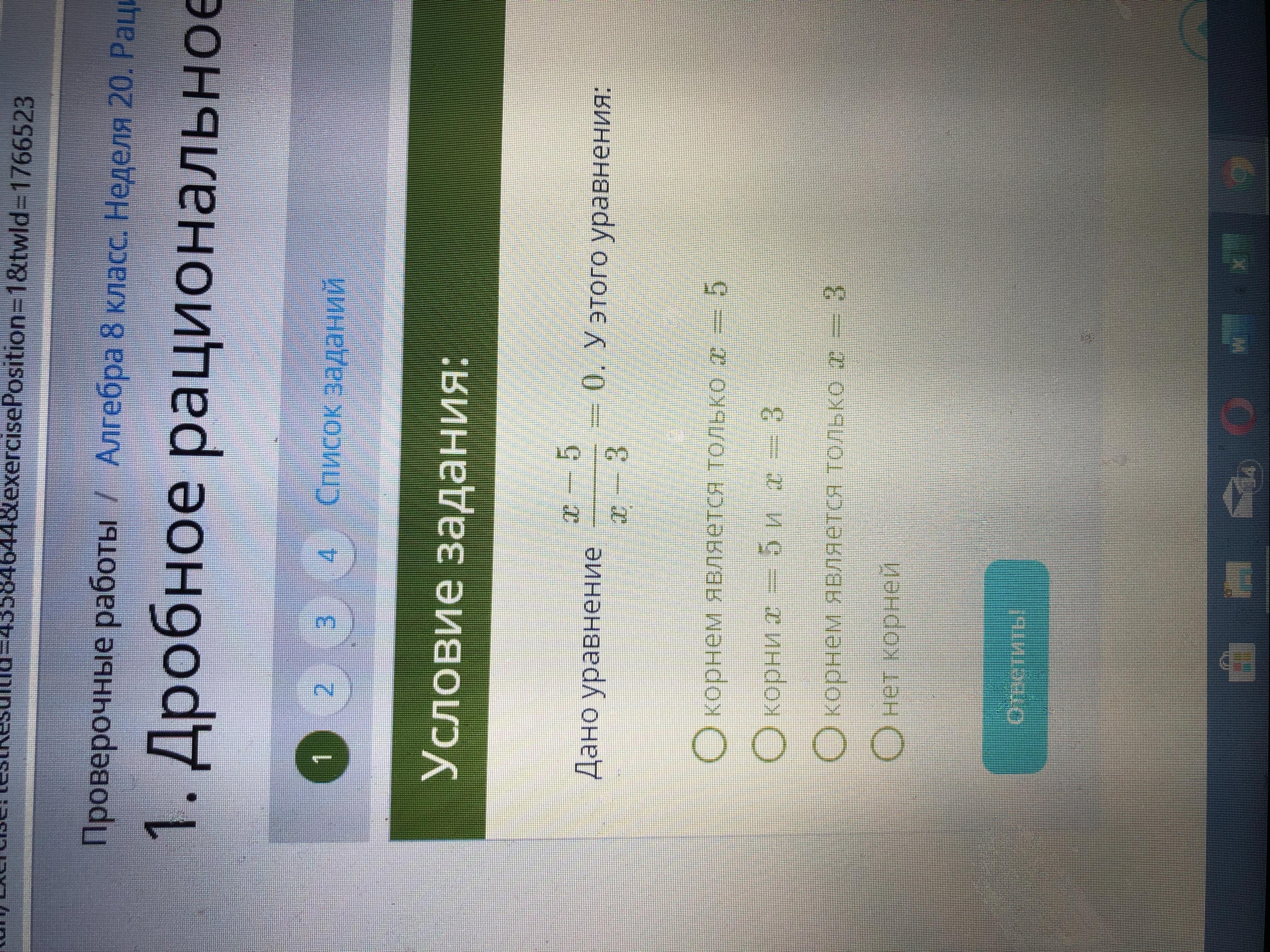
1) Дано уравнение х-5/х-3=0. У этого уравнения:
1. Корнем является только х=5
2. Корни х=5 и х=3
3. Корнем является только х =3
4. Нет корней
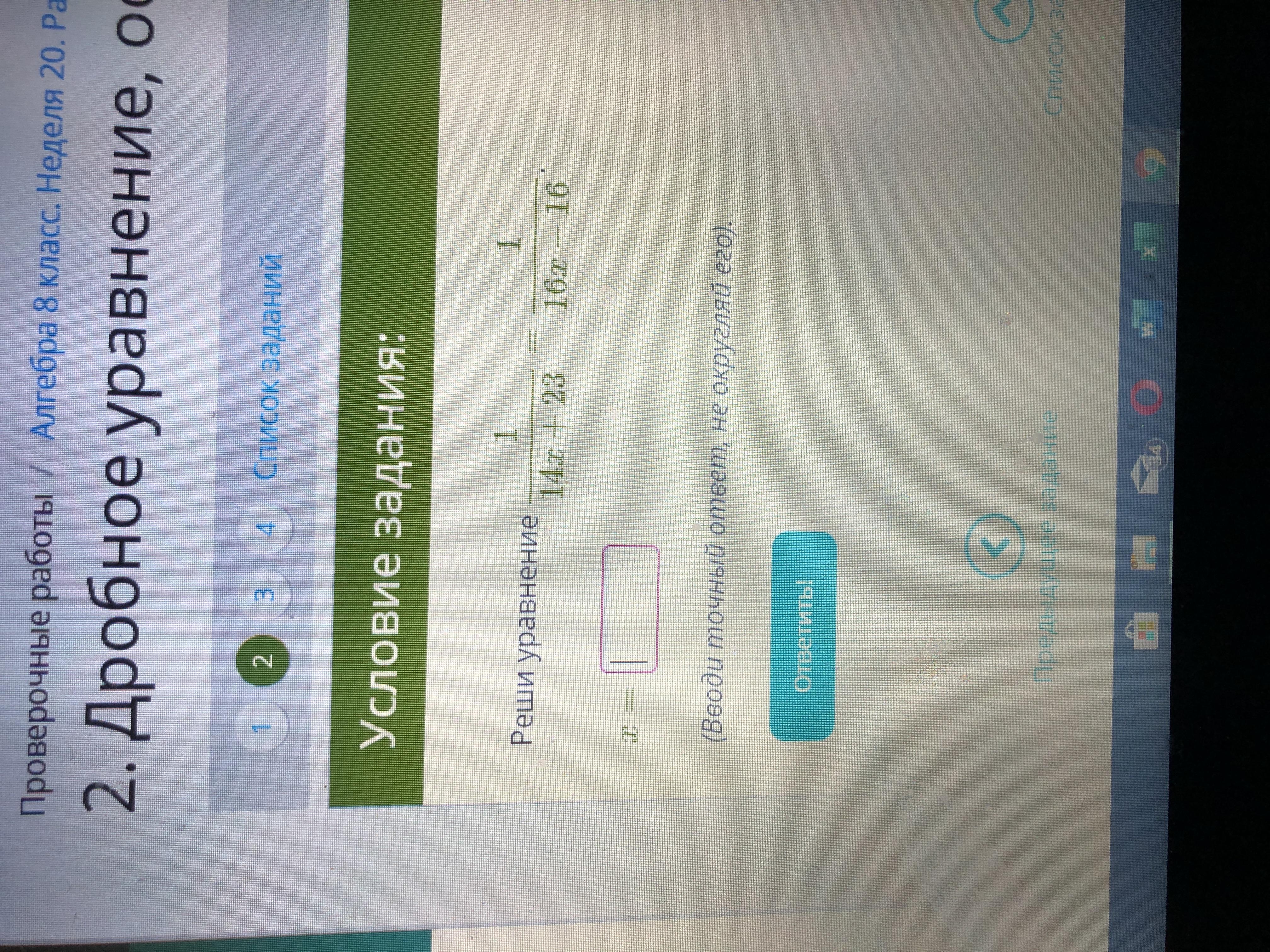
2)Реши уравнение 1/14х+23=1/16х-16
Х=?
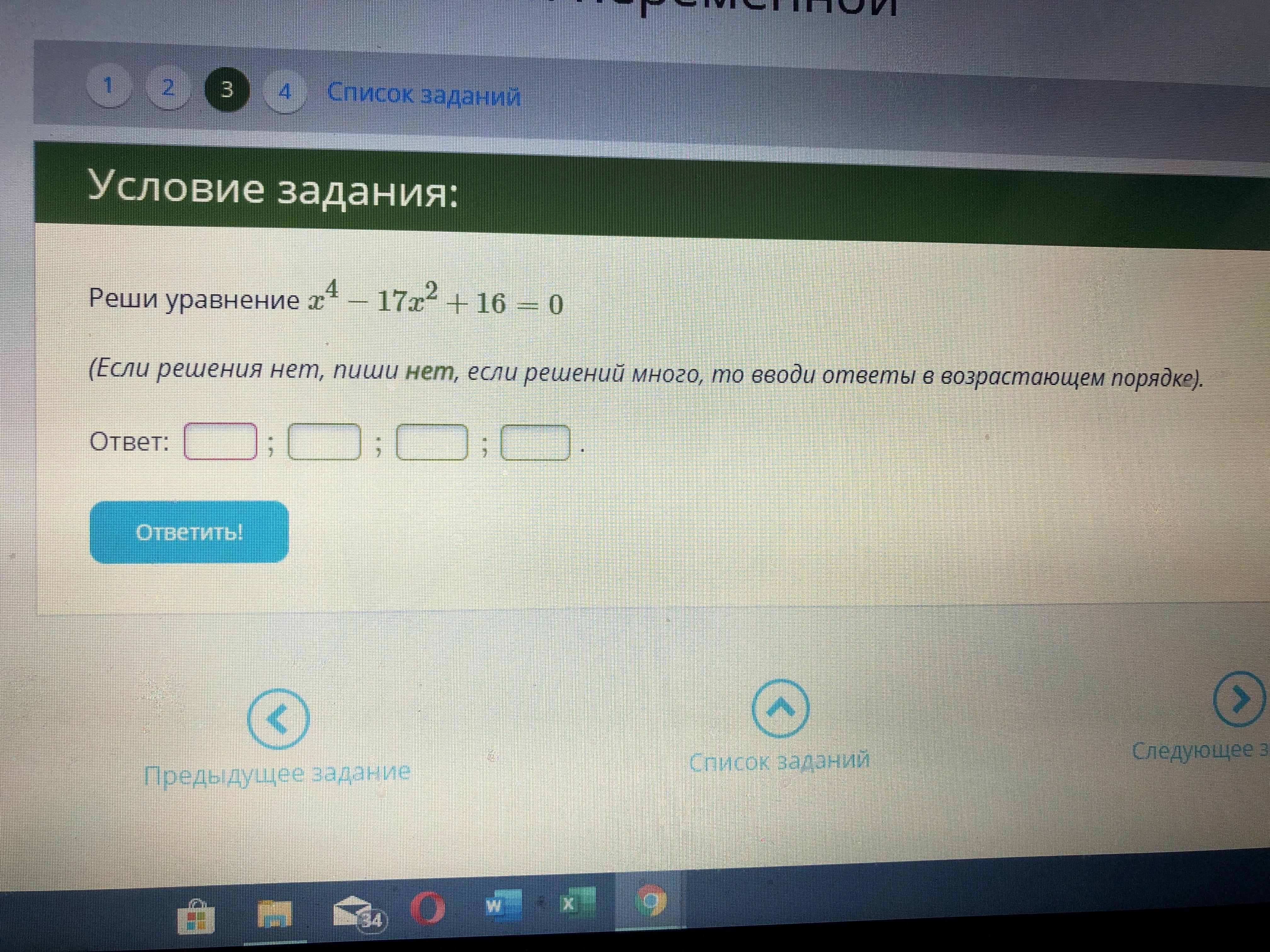
3. Реши уравнение х в 4 ст.-17х в кв.+16=0
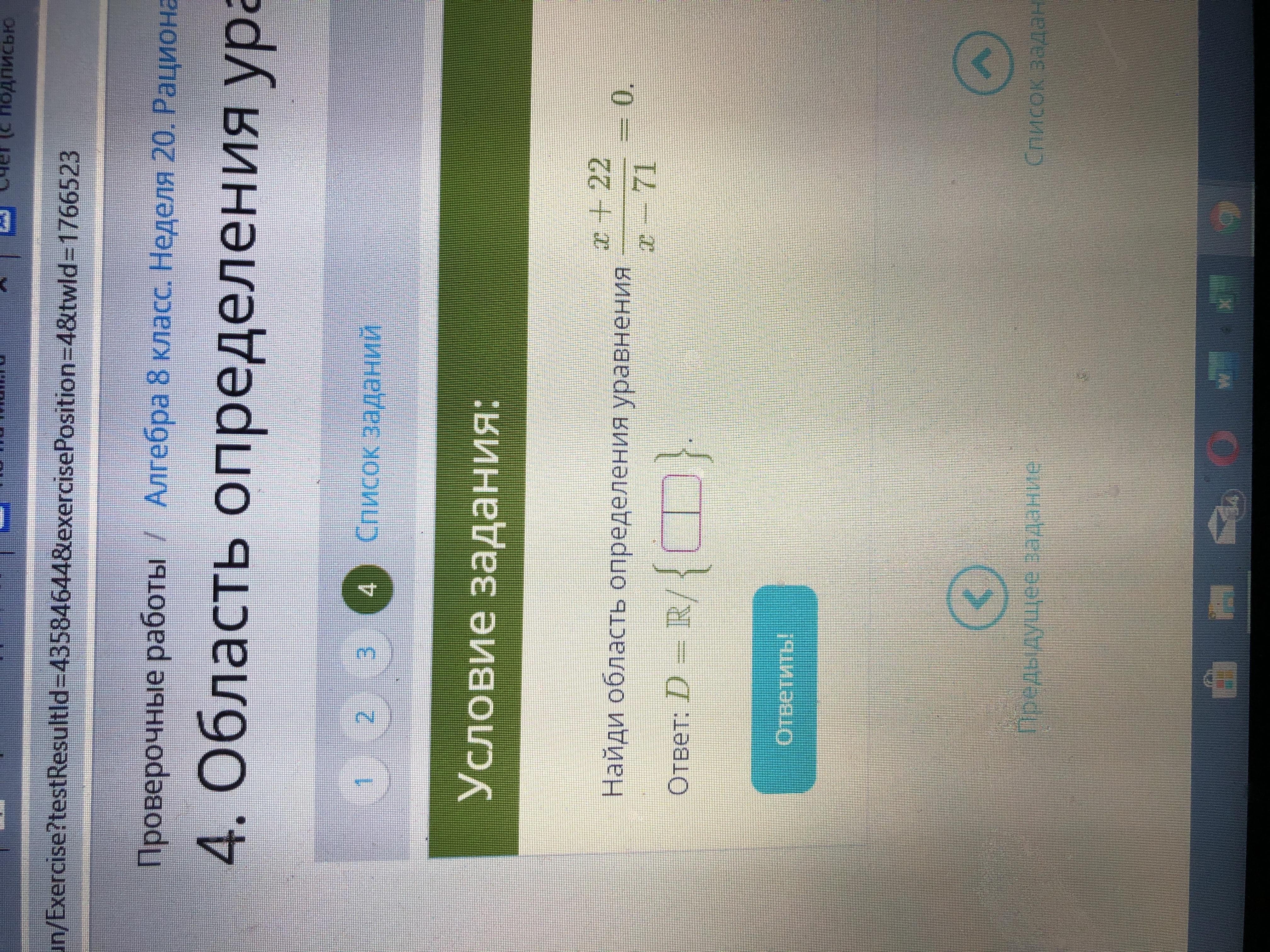
4. Найди область определения уравнения
х+22/х-71=0
Ответ: D=R/ (?)

Answer 1

$1)\; \; \frac{x-5}{x-3}=0\; \; \Rightarrow \; \; \; \left \{ {{x-5=0} \atop {x-3\ne 0}} \right.\; \; \left \{ {{x=5} \atop {x\ne 3}} \right.\\\\Otvet:\; \; x=5\; .$

Корнем является только х=5 . Ответ №1.

$2)\; \; \frac{1}{14x+23}=\frac{1}{16x-16}\; \; ,\; \; \; ODZ:\; \left \{ {{x\ne -\frac{23}{14}} \atop {x\ne 1}} \right.\\\\16x-16=14x+23\; \; ,\; \; 2x=39\; \; ,\; \; x=19,5\\\\3)\; \; x^4-17x^2+16=0\; \; ,\; \; t=x^2\geq 0\; ,\\\\t^2-17t+16=0\; \; ,\; \; t_1=1\; ,\; \; t_2=16\; \; (teorema\; Vieta)\\\\x^2=1\; \; \to \; \; x=\pm 1\\\\x^2=16\; \; \to \; \; x=\pm \\\\Otvet:\; \; -4\; ,\; -1\; ,\; 1\; ,\; 4\; .$

$4)\; \; \frac{x+22}{x-71}=0\\\\x-71\ne 0\; \; \to \; \; x\ne 71\\\\x\in R/\{71\}\; \; ili\; \; \; x\in (-\infty ,71)\cup (71,+\infty )$