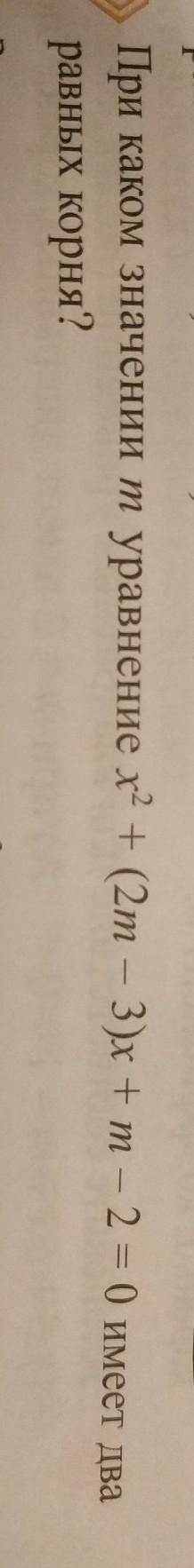Ответы
Ответ дал:
1
Ответ:
m∈R
Пошаговое объяснение:
Данное уравнение является квадратным. Чтобы данное уравнение имело два корня, необходимо, чтобы дискриминант данного уравнения был больше 0.
Найдём корни этого уравнения:
Значит, пересечения с осью Ox нет. Так как коэффициент a при старшей степени > 0, то парабола направленя ветвями вверх, значит, данное уравнение всегда > 0. Следовательно, каково бы ни было m, уравнение имеет два корня.
Вас заинтересует
1 год назад
1 год назад
1 год назад
3 года назад
3 года назад
8 лет назад