В треугольнике одна из сторон равна 5 см, а прилежащие к ней углы равны 40° и 50°. найти с точностью до 0,1 см длины двух других сторон треугольника. Помогите СРОЧНО!! Пожайлуста
Ответы
Ответ дал:
199
Ответ:
см;
см.
Объяснение:
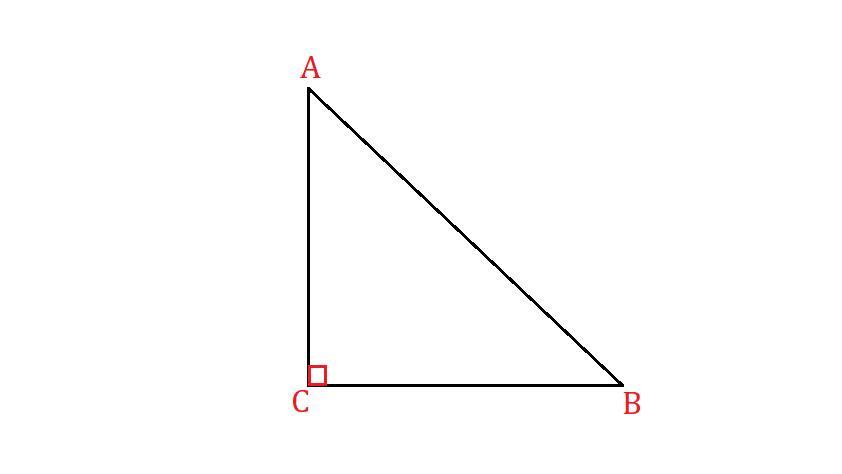
Обозначим данный треугольник буквами
см.
============================================================
- Сумма внутренних углов треугольника равна
Так как - прямоугольный.
По теореме синусов:
Пусть -
см.
По теореме синусов:
Пусть -
см.
Приложения:
Вас заинтересует
1 год назад
1 год назад
1 год назад
3 года назад
3 года назад
9 лет назад