Question

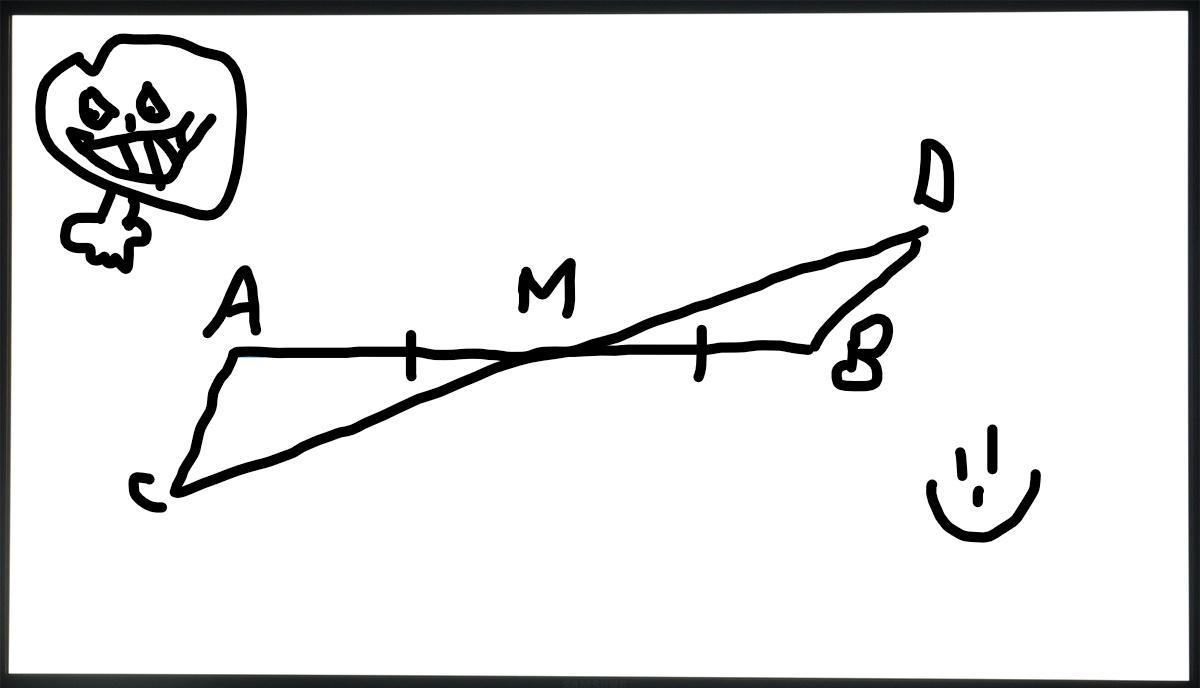
Пацаны пж помогите, AC || BD, M - середина AB. Доказать, что M - середина СD (Доказательство должно быть доходчиво и правильно описано!)

Answer 1

Угол AMC = углу DMB (как вертикальные)

Угол CAM = углу МBD как накрест лежащие при AC || BD и секущей AB. Следовательно, треугольник AMC = треугольнику MBD по стороне и двум прилежащим к ней углам. Из равенства треугольников следует равенство CM = MD, отсюда следует, что М - середина CD