Question

найди угол между диагоналями прямоугольника если известно ,что угол между его диагональю и стороной равен 45 градусов

Answer 1

Дано :

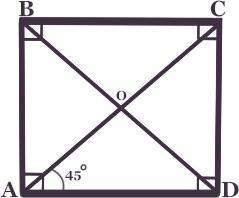
Четырёхугольник ABCD - прямоугольник.

Отрезки АС и BD - диагонали.

Точка О - точка пересечения диагоналей.

∠CAD = 45°.

Найти :

∠AOD = ?

Решение :

∠А = ∠В = ∠С = ∠D = 90° (по определению прямоугольника).

Тогда -

∠OAD + ∠BAO = 90°

∠BAO = 90° - ∠OAD = 90° - 45° = 45°.

Мы получаем, что - ∠BAO = ∠OAD (это значит, что отрезок АС не только диагональ, но и биссектриса ∠А, так как делит этот угол пополам).

• Если в прямоугольнике диагональ является также его биссектрисой, то этот прямоугольник - квадрат.

• Диагонали квадрата взаимно перпендикулярны.

Тогда получаем, что -

∠AOD = 90°.

Ответ :

90°.