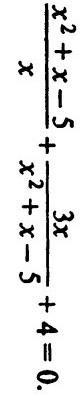Ответы
Ответ дал:
1
Ответ:
решение на фотографии
Приложения:

mathgenius:
Зачем так сложно? (x^2+x-5)/x=t
Ответ дал:
1
Вас заинтересует
1 год назад
1 год назад
3 года назад
8 лет назад