Ответы
Ответ дал:
1
Ответ:
Пошаговое объяснение:
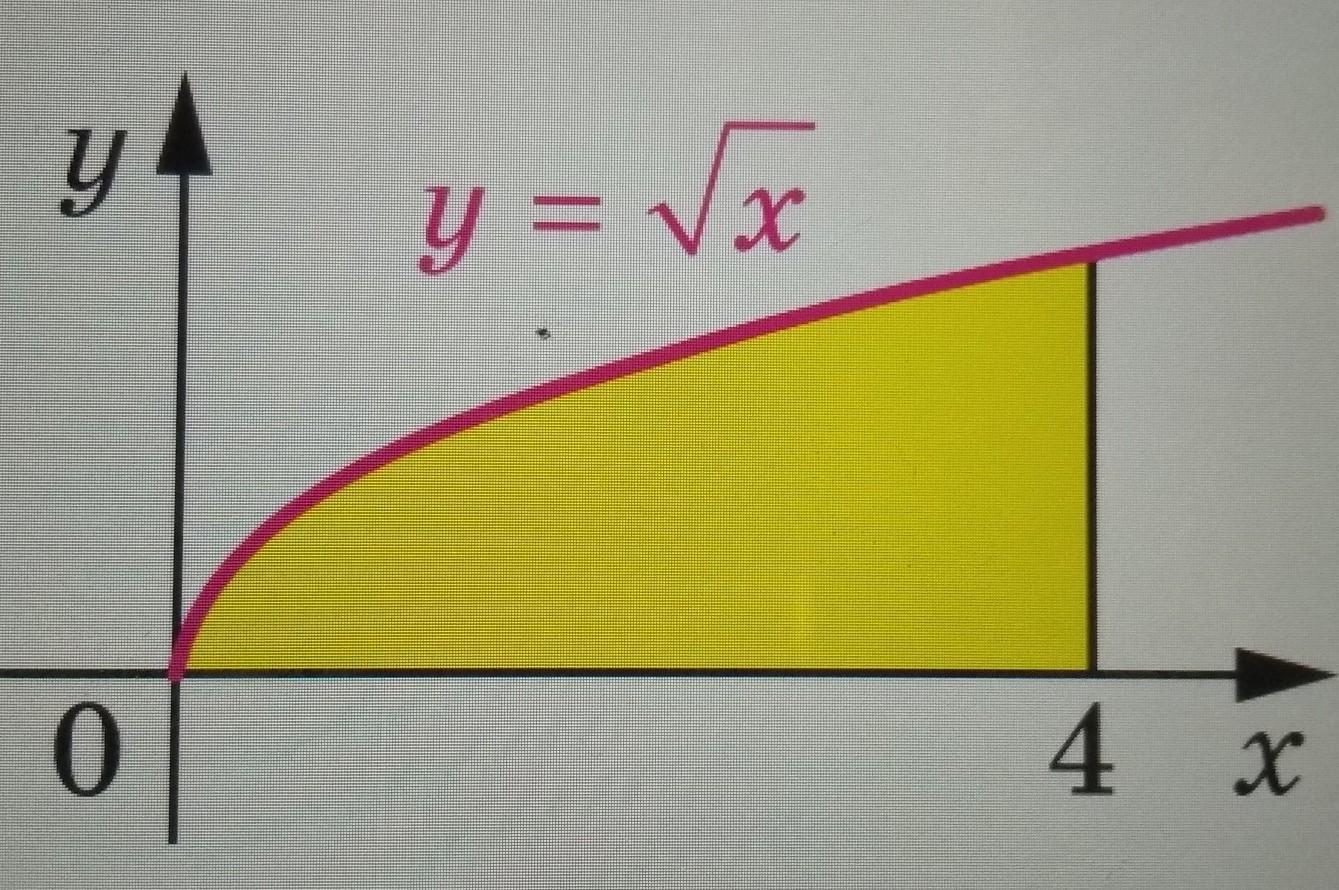
** j - интеграл
площадь вычисляется с помощью определенного интеграла. пределы интегрирования от 0 до 4
Вас заинтересует
1 год назад
1 год назад
1 год назад
3 года назад
9 лет назад
9 лет назад