Ответы
Ответ дал:
1
, значит
уравнение прямой по точке и угловому коэффициенту:
- BC
B - точка пересечения AB и BC
E - середина BC
- CD
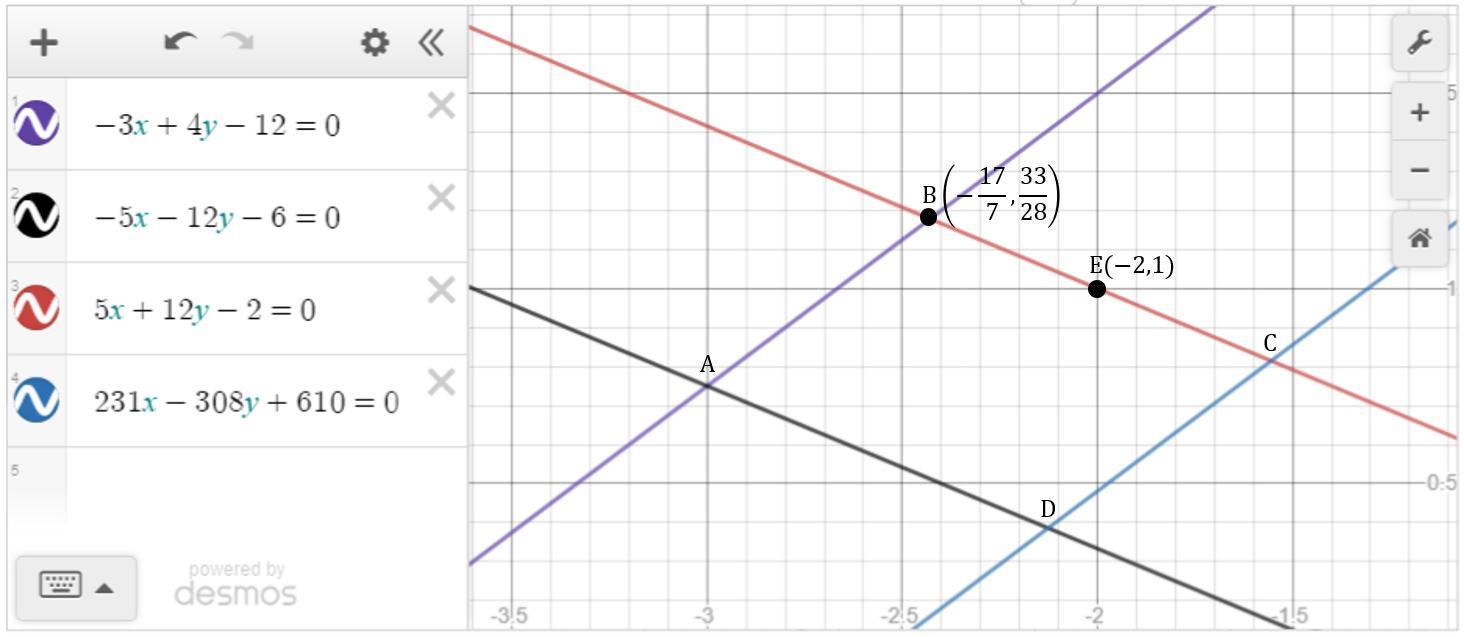
чертёж для наглядности:
Приложения:
Вас заинтересует
1 год назад
1 год назад
2 года назад
2 года назад
3 года назад
9 лет назад
