Question

Найдите радиус окружности , вписанной в равнобедренный треугольник с основанием, равным 12 см, и боковой стороной , равной 10 см

Answer 1

Ответ:

$3$ см.

Объяснение:

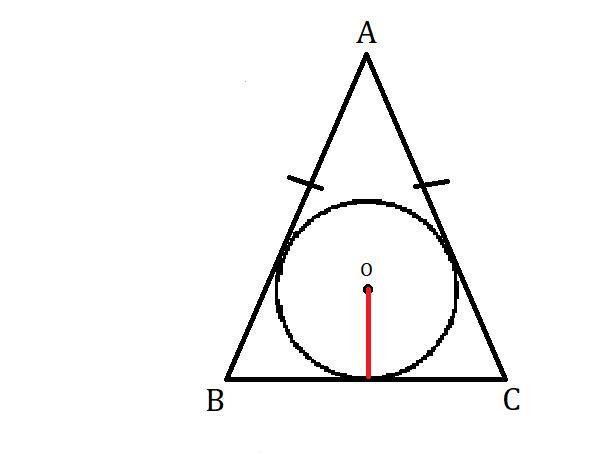
Обозначим данный равнобедренный треугольник буквами $ABC$.

Пусть $AB = 10$ см, $BC=12$ см.

=======================================================

Радиус вписанной окружности равнобедренного тр-ка находится по формуле:

$R=\dfrac{BC}{2}\sqrt{\dfrac{2AB-BC}{2AB+BC}}$

--------------------------------------------------------------------

$\Rightarrow R=\dfrac{12}{2}\sqrt{\dfrac{2\cdot10-12}{2\cdot10+12}}=6\sqrt{\dfrac{8}{32}}=6\sqrt{\dfrac{1}{4}}=6\cdot\dfrac{1}{2}=\dfrac{6}{2}=3$ см.

Answer 2

Ответ:

решение представлено на фото

Объяснение: