Алгебра! Помогите, очень срочно..
Приложения:
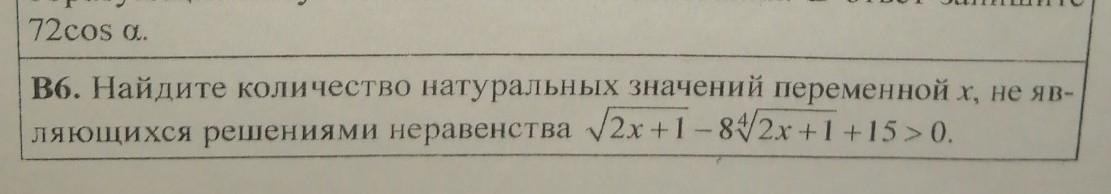
MrSolution:
вот тебе промежуток [40; 312]. Итого 273 вроде бы.
312-40=272
если я правильно количество решений считаю
Ну, смотри, вот есть числа 1,2,3. 3-1=2, но чисел-то 3. Поэтому ещё +1
логично, спасибо большое
Срочно! Помогите пожалуйста, геометрия!
https://znanija.com/task/34033987?utm_source=android&utm_medium=share&utm_campaign=question
https://znanija.com/task/34033987?utm_source=android&utm_medium=share&utm_campaign=question
Ответы
Ответ дал:
0
Ответ:272 натуральных числа не являются решением неравенства
Объяснение:
Пусть ⁴√2х+1=у, тогда: у²-8у+15>0, (у-5)(у-3)>0, у∈(-∞:3)∪(5;+∞).
⁴√2х+1<3 или ⁴√2х+1>5 Возведём обе части неравенства в 4 степень
2х+1< 81 или 2х+1>625
2х<80 или 2х>624
х<40 или х> 312
312- 39=273 - число натуральных чисел, не являющихся решением неравенства.
Ответ: 273
В ответе снизу 271, в ответе сверху 272. А у меня 273 выходило... Так что верно?
273
Ответ дал:
0
Ответ:
273
Объяснение:
Т.к по условию просят найти количество чисел, не являющихся решением неравенства, поменяем знак:
Замена:
Тогда:
За чертой:
Начертим картинку:
•-0.5 --- + --•3 ---- - ---•5--- + -->t
Тогда после обратной замены нас устраивает:
•-0.5 --- + --•40 ---- - ---•312--- + -->x
Знак в неравенстве <=. Значит решение неравенства:
Тогда ответ на задачу:
Вас заинтересует
1 год назад
1 год назад
1 год назад
3 года назад
3 года назад