Ответы
Ответ дал:
0
Ответ: BD = 8√5, AC = 4√5
Объяснение:
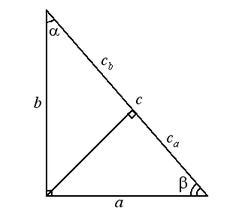
Рассмотрим прямоугольный треугольник АОВ. Высота ОК делит гипотенузу на отрезки, называемые проекциями катетов.
Зная формулы расчета этих отрезков (формулы во вложении), можно найти катеты АО и ВО.
Т.к. диагонали точкой пересечения делятся пополам,
BD = 2*BO = 8√5
AC = 2*AO = 4√5
Приложения:

Вас заинтересует
1 год назад
1 год назад
2 года назад
2 года назад
3 года назад
3 года назад
9 лет назад
9 лет назад
