Ответы
Ответ дал:
0
Объяснение: ОДЗ: x² - 2 ≥ 0, x ∈ (-∞; -√2)∪(√2; +∞) (во вложении)
Обе части возведем в квадрат:
ОДЗ удовлетворяют только два корня: х = -3 и х = 1 + √2.
Приложения:
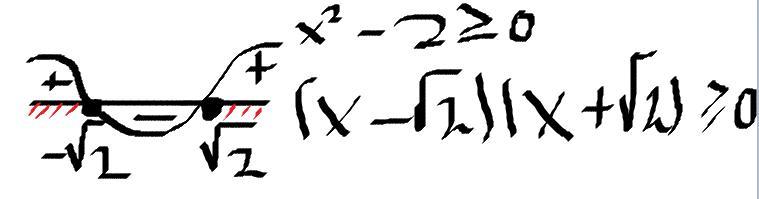
terikovramazan:
проверь х=3
забыл -. Спасибо
Ответ дал:
0
Ответ: приложено
Объяснение:
Приложения:

Вас заинтересует
1 год назад
1 год назад
1 год назад
3 года назад
8 лет назад