Ответы
Ответ дал:
1
Ответ:
Задача 4: 6
Задача 5: 12
Объяснение:
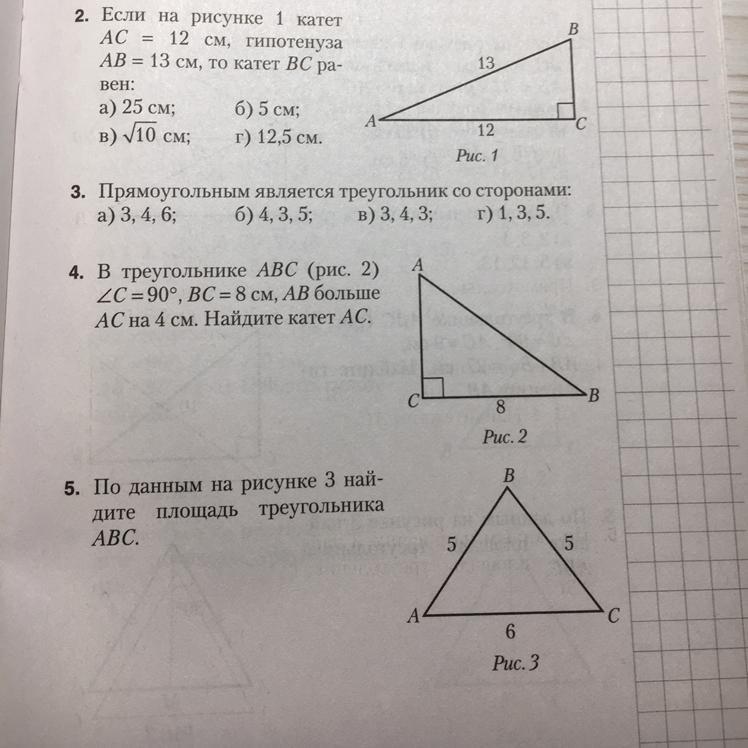
4) Примем катет АС за х, а гипотенузу АВ за х+4, тогда по формуле Пифагора:
(х+4)² = х² + 8²
х² + 8х + 16 = х² + 64
Сокращаем х² и переносим 16 в другую сторону
8х = 48
х = 48/8
х = 6
5) Находим площадь треугольника по формуле Герона:
S = √(p·(p - a)·(p - b)·(p - c))
Где р - полупериметр треугольника (a+b+c)/2
S = √(8*3*3*2) = √(16*9) = √(4²*3²) = 4*3 = 12
Ответ: S = 12
jetblackhorror86:
Спасибо, но формулу Герона мы ещё не брали)
Тогда можешь провести к основанию высоту и т.к. у тебя боковые стороны равны 5, то по правилу равнобедренного треугольника это и высота и медиана. Она поделит основание 6 на 2 и в итоге будет две части по 3. Как ты видишь - большой треугольник поделился таким образом на 2, да не простых, а египетских, т.к. у тебя один катет равен 3, а гипотенуза 5, то тогда другой катет равен 4. Тут уже действует старая добрая 1/2*основание*высоту (либо же полупроизведение катетов, умноженное на 2)
Вас заинтересует
1 год назад
1 год назад
2 года назад
2 года назад
3 года назад
3 года назад
9 лет назад
9 лет назад