Ответы
Ответ дал:
85
Ответ:
Объяснение:
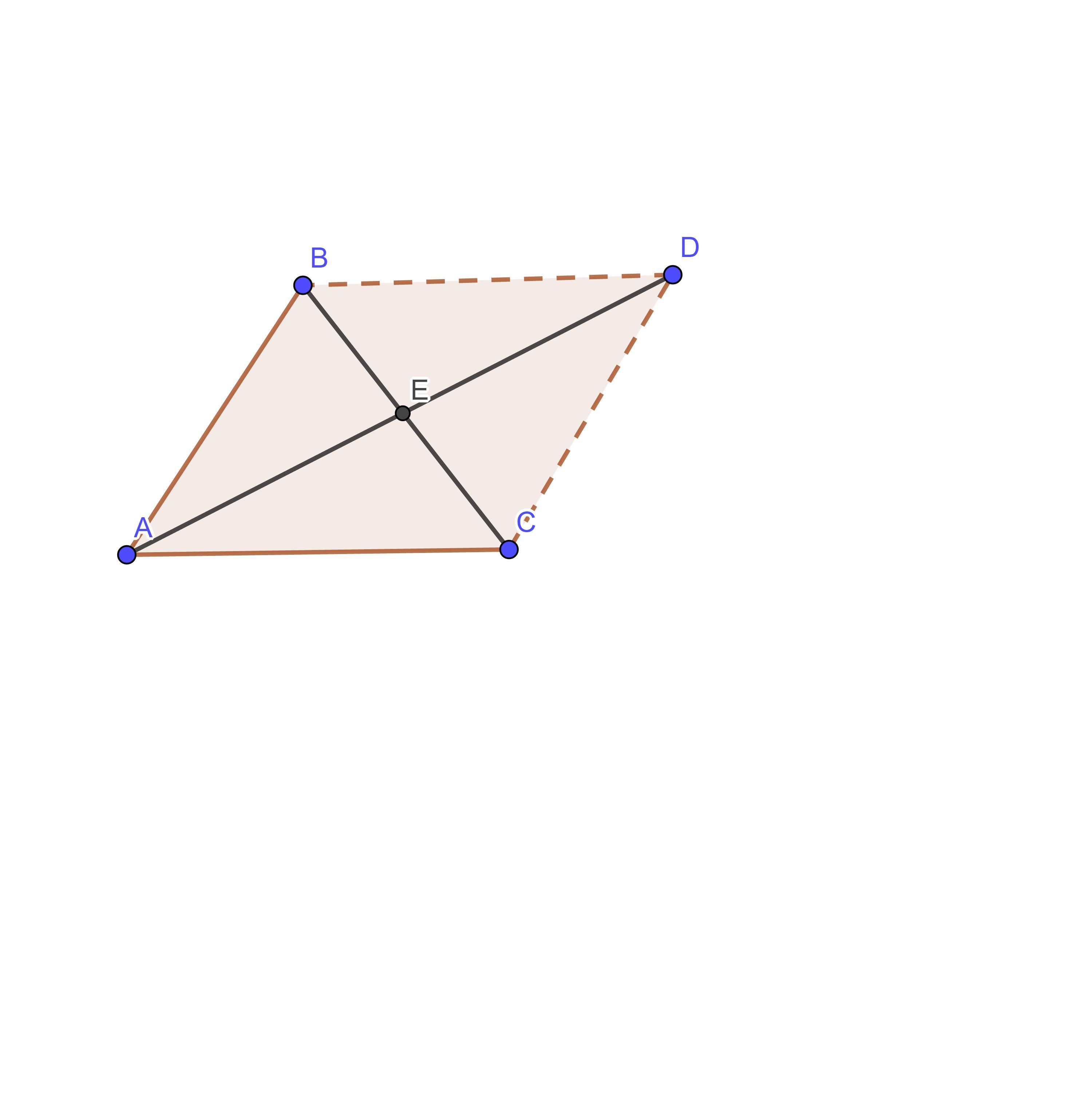
В Δ ABC AB=2 см, AC= 3 см, BC=4 см. Проведем медиану AE к стороне BC. Найдем медиану AE, для этого достроим Δ ABC до параллелограмма ABDC. По свойству квадратов диагоналей параллелограмма : сумма квадратов диагоналей параллелограмма равна сумме квадратов его сторон.
Так как диагонали параллелограмма пересекаясь, точкой пересечения делятся пополам, то AD= 2AE.
Приложения:
Вас заинтересует
1 год назад
1 год назад
1 год назад
3 года назад
3 года назад
8 лет назад