Question

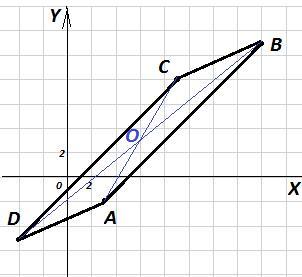
Найдите координаты вершины B параллелограмма ABCD, если A (3; −2),
C (9; 8), D (−4; −5).​

Answer 1

У параллелограмма диагонали точкой пересечения делятся пополам. Пусть точка О - точка пересечения диагоналей, то есть середина отрезка AC и середина отрезка BD.

$X_O=\dfrac{X_A+X_C}2=\dfrac{3+9}2=6\\\\Y_O=\dfrac{Y_A+Y_C}2=\dfrac{-2+8}2=3\\\\X_O=\dfrac{X_B+X_D}2\\\\X_B=2X_O-X_D=2\cdot 6-(-4)=16\\\\Y_O=\dfrac{Y_B+Y_D}2\\\\Y_B=2Y_O-Y_D=2\cdot 3-(-5)=11$

Ответ : (16; 11)

Answer 2

Если АВСD - параллелограмм, то векторы АВ и DС равны, ВС и АD равны. Везде над векторами надо ставить стрелки или черточки.

Пусть В(х;у), найдем координаты точки В предварительно определив координаты векторов АВ и DС, вычитая для каждого из координат конца координаты начала вектора.

АВ(х-3;у+2)

DС(9+4;8+5);

х-3=13

у+2=13

х=16

у=11

ВС(9-х;8-у)=АD(-7;-3)⇒9-х=-7;х=16;

8-у=-3; у=16

Значит В(16;11)