Помогите дорешать задачку)
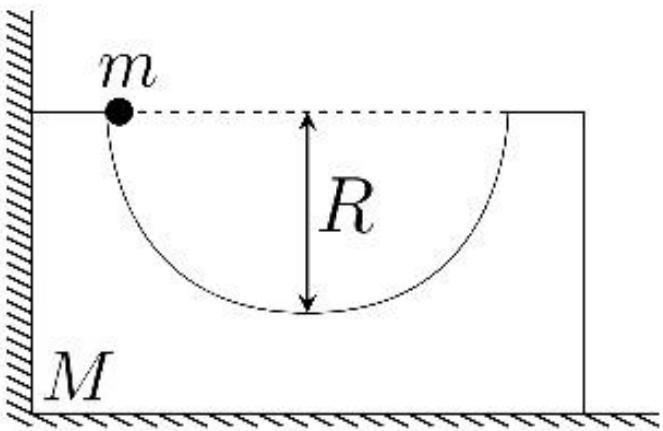
Груз массы m= 1 кг находится в верхней точке желоба,имеющего сферическую форму. Масса желоба M= 2 кг , радиус сферической поверхности R= 10 см .Найдите, на какую максимальную высоту H поднимется груз после прохождения нижней точки один раз. Ответ приведите в сантиметрах, округлив до десятых.

Формула через которую можно решить:
mgR=mv²/2 => v = √(2gR)
mv = (m+M)u
(m+M)u²/2 + mgH = mv²/2

Приложения:

Persianka: Это разве не 9 класс?

dfghdfghf: нет))мы такого даже не проходили с 3 переменными

Persianka: Или у Вас физика не по Перышкину, а по Грачеву? И тогда 7 класс?

dfghdfghf: перышкин))но мы такого не проходили что 3 переменных

dfghdfghf: решите УМОЛЯЮ ВАС.... пожалуйста....

dfghdfghf: так не могли бы проверить задачу, я ее решил, нужно ваше мнение правильно или нет:
вот условие:
Доска плотности ρ1= 500 кг/м^3 объемом V= 0.1 м^2 плавает в воде. Груз какой массы можно положить на доску сверху, чтобы система не утонула. Плотность воды ρ0= 1000 кг/м^3, плотность груза ρ2= 1500 кг/м^3, ускорение свободного падения g=10 м/с^2. Ответ приведите в килограммах, округлив до целых.

ответ:
150 кг

dfghdfghf: вот формулы
ρ1*V1*g + ρ2*V2*g = ρ0*g*(V1+V2)
m2 = ρ2*V2

dfghdfghf: проверьте пожалуйста))умоляю вас

Persianka: Смотря что считать под словом "не утонула". Странно, когда и доска и груз оба под водой и считается что "не утонула". Я бы взяла вместо (V1+V2) только объем доски V1. В остальном все верно.

dfghdfghf: не утонула система(то есть доска и груз) ну ответ верный)