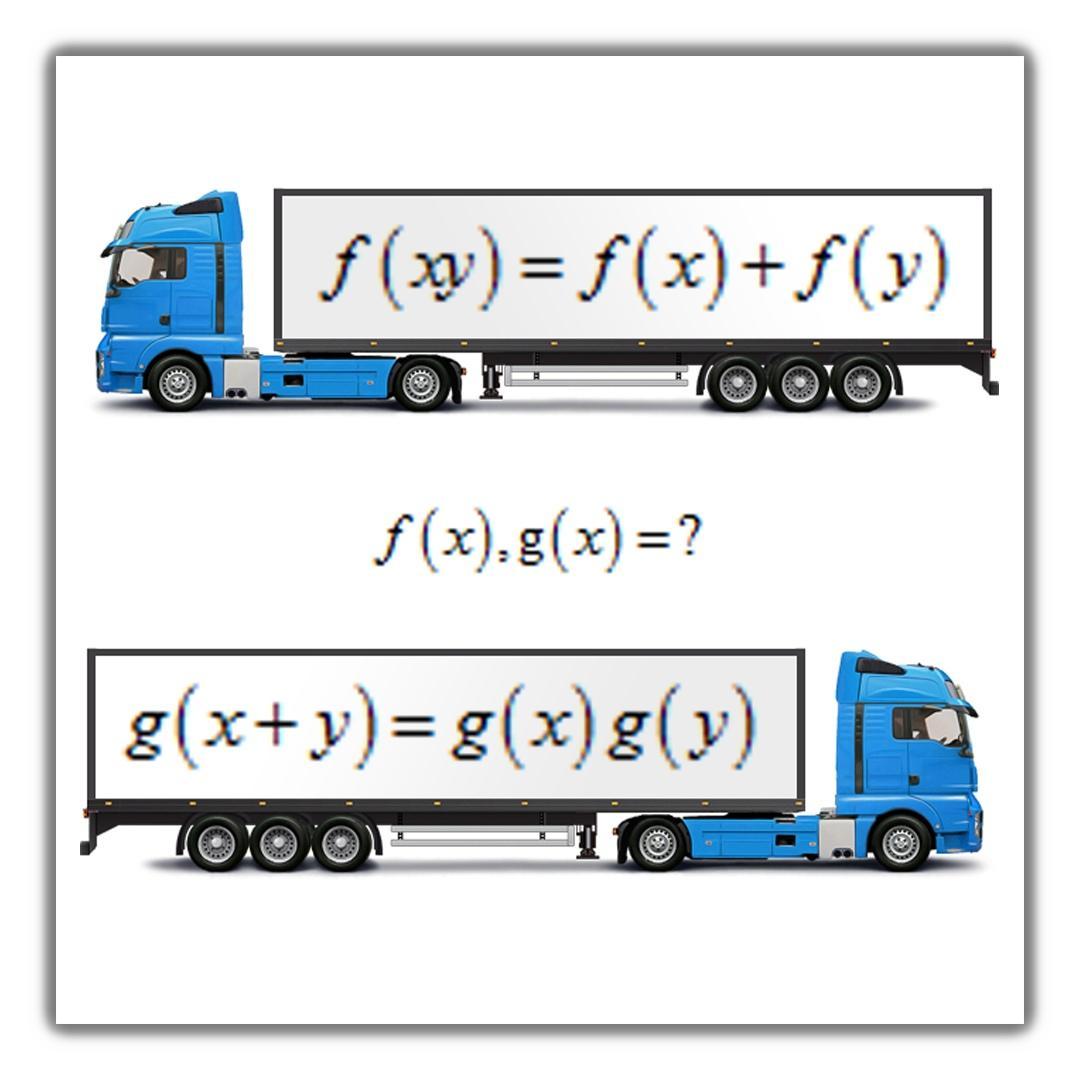
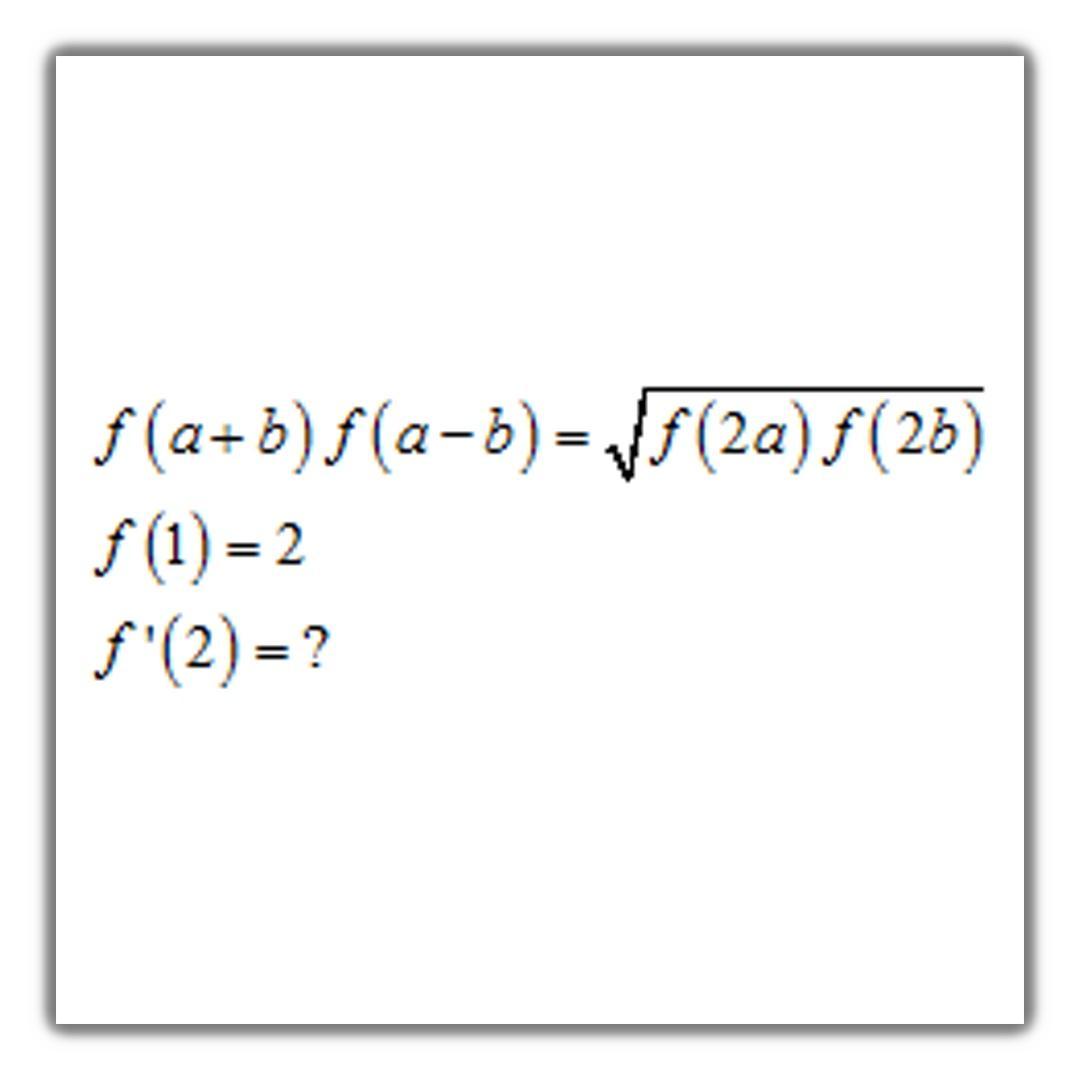Ответы
2.
Введем функцию
Тогда
Т.е. удовлетворяет функциональному уравнению Коши. А значит
(в классе непрерывных функций других решений нет).
Тогда
3. Если в область определения входит 0, то
- единственное решение.
Пусть функция не определена в 0.
Тогда для удобства ограничим область определения функции положительными числами (а при отрицательном значении аргумента функция примет модуль числа)
Т.е. удовлетворяет функциональному уравнению Коши. А значит
(в классе непрерывных функций других решений нет).
Вернем исходную область определения функции, заменив переменную на ее модуль:
4. Очевидно, что - одно из решений.
Пусть
Значит можно логарифмировать
Т.е. удовлетворяет функциональному уравнению Коши. А значит
(в классе непрерывных функций других решений нет).