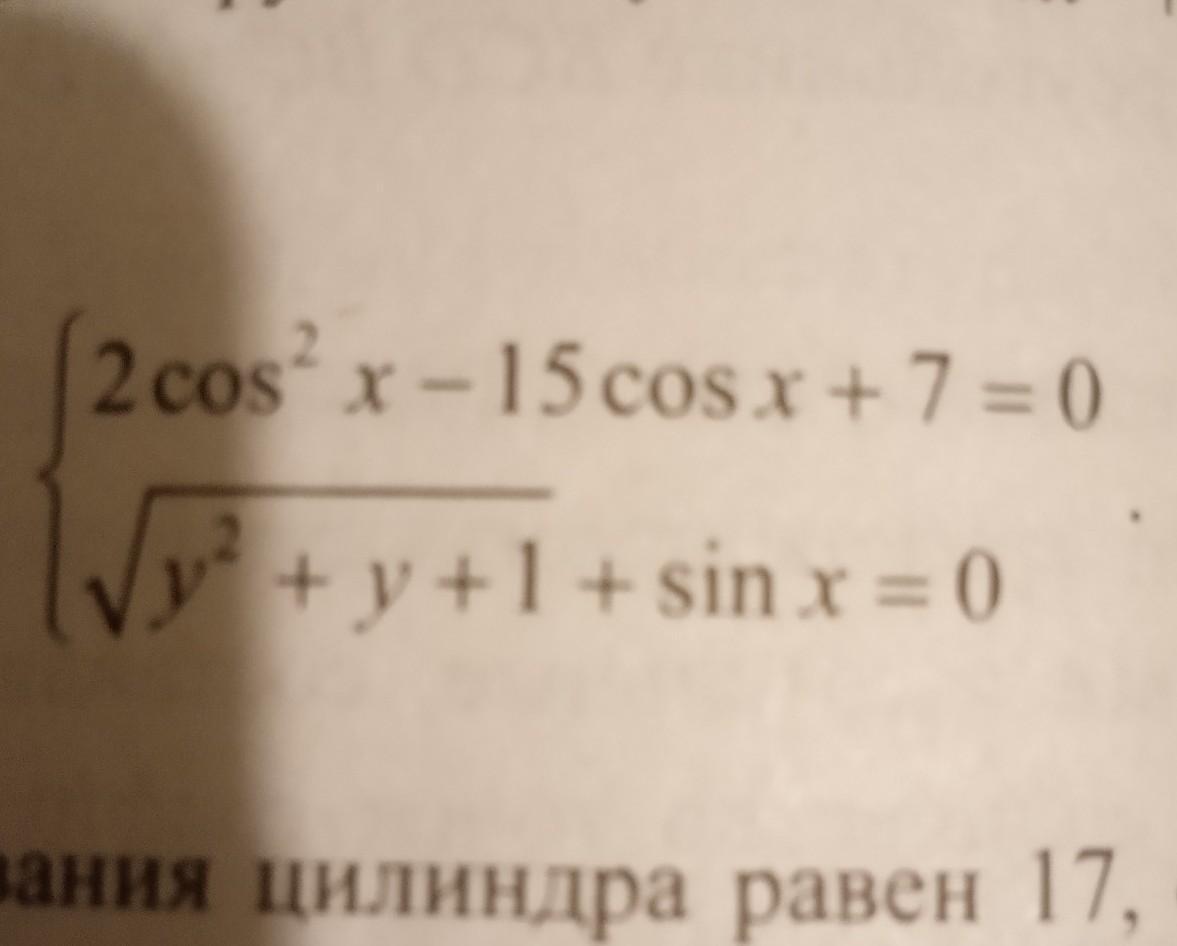Ответы
Ответ дал:
0
Ответ:
в объяснении
Пошаговое объяснение:
Решим 1е уравнение системы как квадратное
не имеет решений
x=π/3+2πn; x=-π/3+2πn; n∈Z
Из второго уравнения системы получаем, что
(π/3+2πn;-1/2); (-π/3+2πn;-1/2) n∈Z
Вас заинтересует
1 год назад
1 год назад
1 год назад
1 год назад
3 года назад
3 года назад
8 лет назад