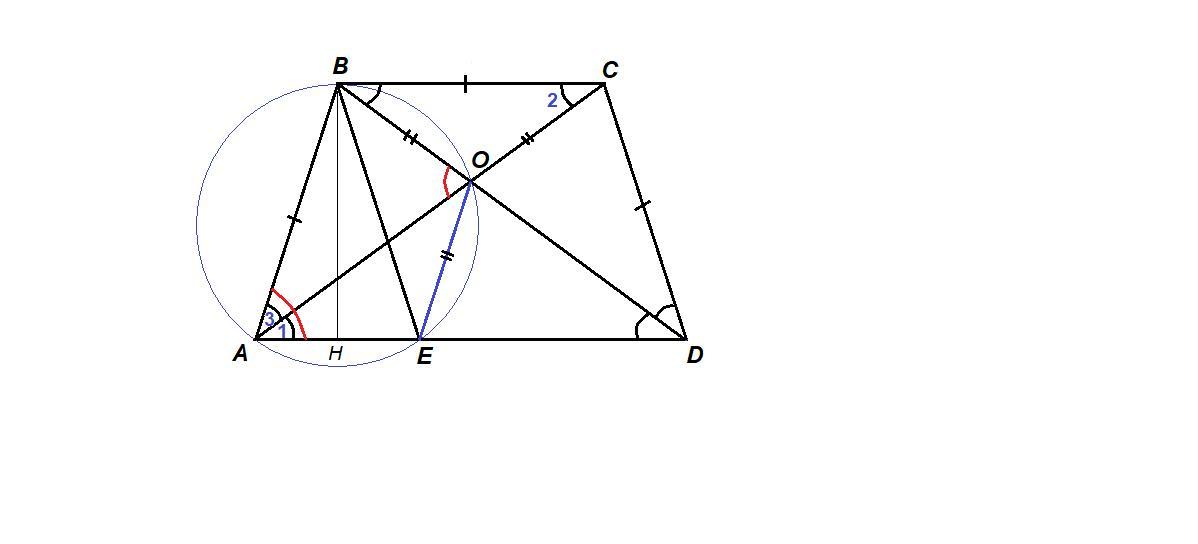
Дана трапеция ABCD (AB=BC=CD=3). O – точка пересечения диагоналей AC и BD. Окружность, описанная вокруг треугольника ABO, пересекает основание AD повторно в точке E. Найдите максимум OE•AC.
Ответы
Ответ:
9
Объяснение:
∠1 = ∠2 как накрест лежащие при пересечении AD║ВС секущей АС,
∠2 = ∠3 как углы при основании равнобедренного треугольника АВС (АВ = ВС по условию), ⇒
∠1 = ∠3.
Эти углы вписанные. Раз они равны, то равны и дуги, на которые они опираются, ∪ВО = ∪ОЕ. А равные дуги стягиваются равными хордами, значит ВО = ОЕ.
___________
∠BDA = ∠CBD как накрест лежащие при пересечении AD║ВС секущей BD,
∠CBD = ∠CDB как углы при основании равнобедренного треугольника BCD, ⇒
∠BDA = ∠CDB.
Трапеция равнобедренная, значит ∠BAD = ∠CDA, а значит равны между собой и все углы, помеченные одной черной дужкой. Тогда
ОЕ = ОВ = ОС.
_______
∠ВОА = 2 · ∠2 как внешний угол ΔВОС,
∠ВАD = 2 · ∠1,
а так как ∠1 = ∠2, то и ∠ВОА = ∠BAЕ.
Эти углы вписанные, значит равны соответствующие дуги (∪ВА = ∪ВЕ) и стягивающие их хорды ВА = ВЕ, ⇒ ΔАВЕ равнобедренный.
________
ВН - высота трапеции и высота ΔАВЕ, вписанного в ту же окружность. Так как треугольник равнобедренный, центр окружности лежит на высоте ВН, а так как ВН⊥ВС, то ВС - касательная к окружности.
По свойству отрезков касательной и секущей, проведенных из одной точки:
BC² = CO · CA = 9
CO = OE, значит
ОЕ · АС = 9 - значение постоянное