Найдите отношение двух сторон треугольника, если его медиана, выходящая из их общей вершины, образует с этими сторонами углы в 30∘ и 90∘.
помогите, очень-очень срочно!
Ответы
Ответ дал:
1
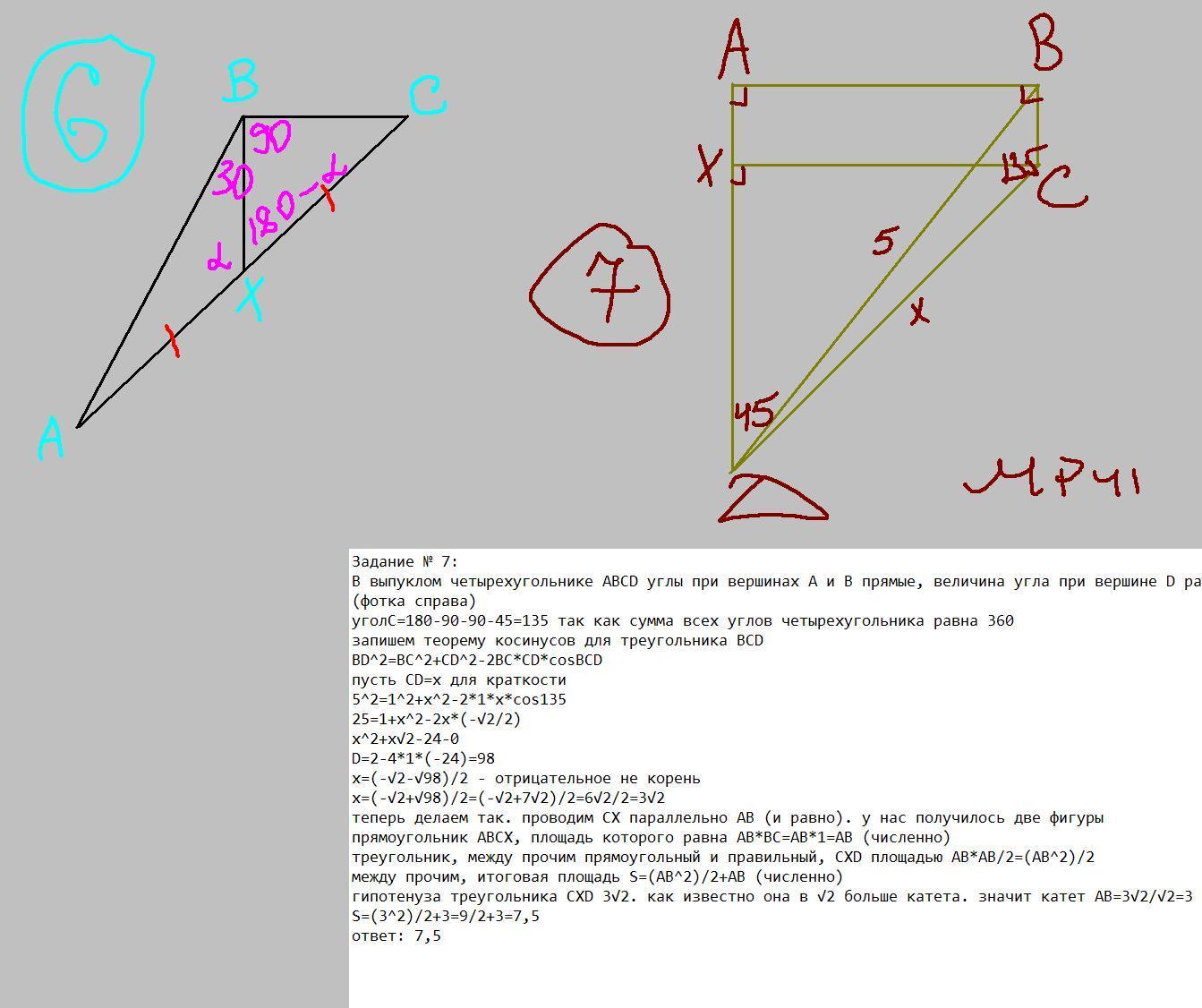
(фотка слева)
от нас хотят ВС/АВ (или обратное)
для треугольника АВХ запишем теорему синусов:
AX/sinABX=AB/sinAXB
Выразим так: AXsinAXB=ABsinABX
для треугольника CВХ запишем теорему синусов:
CX/sinCBX=BC/sinCXB
Выразим так: CXsinCXB=BCsinCBX
между прочим:
1) AX=CX так как проведена медина BX
2) sinAXB=sinCXB так как синусы смежных углов равны
значит AXsinAXB=CXsinCXB
значит ABsinABX=BCsinCBX
BC/AB=sinABX/sinCBX
BC/AB=sin30/sin90
BC/AB=(1/2)/1
BC/AB=1/2
ответ: 1/2
Приложения:
Вас заинтересует
1 год назад
1 год назад
1 год назад
3 года назад
8 лет назад