Question

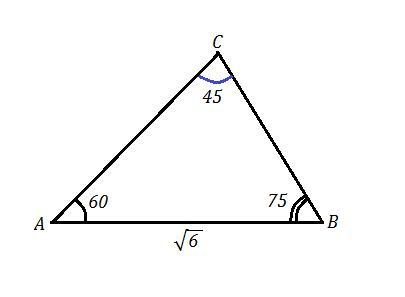
Одна из сторон треугольника равна ✓6, а прилегающие к ней углы - 60° и 75°. Найдите вторую сторону треугольника, которая прилегает к углу 75° Варианты ответа: 4 см, 1 см, 3 см, 2 см

Answer 1

Ответ:

Дано:  ΔАВС.  АВ=√6 , ∠А=60°  ,  ∠В=75° . Найти: ВС.

Найдём ∠С=180°-60°-75°=45° .

Применим теорему синусов:

$frac{AB}{sinC}=frac{BC}{sinA} ; ; to ; ; ; frac{sqrt6}{sin45^circ }=frac{BC}{sin60^circ } ; ; ,; ; frac{sqrt6}{frac{sqrt2}{2}}=frac{BC}{frac{sqrt3}{2}}; ; ,; ; frac{2sqrt6}{sqrt2}=frac{2cdot BC}{sqrt3}; ,\\BC=frac{sqrt3cdot sqrt6}{sqrt2}=frac{sqrt3cdot (sqrt3cdot sqrt2)}{sqrt2}=sqrt3cdot sqrt3=3$

Answer 2

Решение рисую акварелью)), во вложении см.