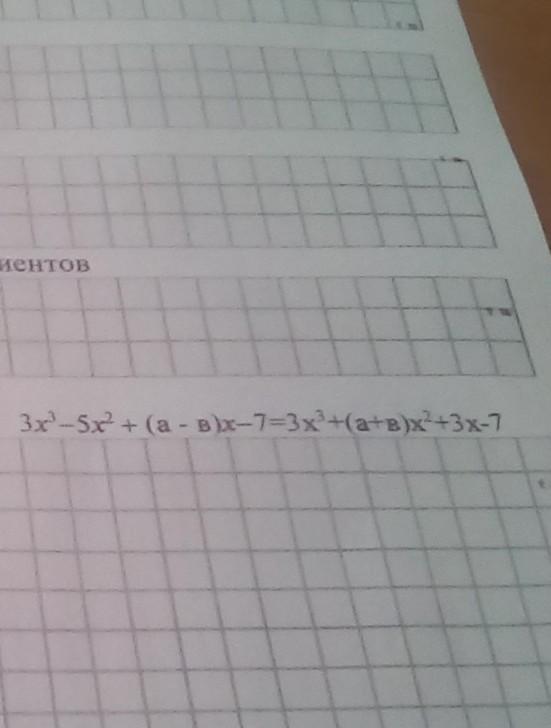Ответы
Ответ дал:
0
Это равенство должно быть верным.
Значит,
ПРОВЕРКА:
Ответ: a = -1; b = -4
Вас заинтересует
2 года назад
2 года назад
3 года назад
3 года назад
9 лет назад
9 лет назад
9 лет назад