исследовать на сходимость ряда (-1)^n+1×1/ n^1/2. n в корне, просто незнаю как записать пишу так: n^1/2
Приложения:
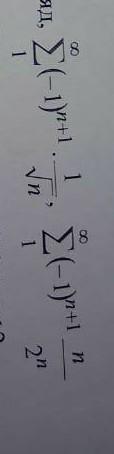
Ответы
Ответ дал:
0
1)
2) , а значит функция
монотонно убывает. Тогда
3)
Тогда ряд сходится по признаку Лейбница
Ответ дал:
0
Обобщённым гармоническим рядом с k=1/2≤1, просто сказать про гармонический недостаточно
Ответ дал:
0
ок
Вас заинтересует
2 года назад
2 года назад
9 лет назад
9 лет назад
9 лет назад