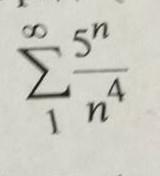Question

исследовать на сходимость
5^n/n^4​

Answer 1

$limlimits_{ntoinfty}dfrac{5^n}{n^4}=left[dfrac{infty}{infty}right]=limlimits_{ntoinfty}dfrac{ln5cdot5^n}{4n^3}=limlimits_{ntoinfty}dfrac{ln^25cdot5^n}{4cdot3cdot n^2}=limlimits_{ntoinfty}dfrac{ln^35cdot5^n}{4cdot3cdot2cdot n}=\ limlimits_{ntoinfty}dfrac{ln^45cdot5^n}{4cdot3cdot2}=inftyneq 0$

Необходимое условие сходимости не выполнено, а значит ряд расходится

2 способ

$limlimits_{ntoinfty}sqrt[n]{dfrac{5^n}{n^4}}=limlimits_{ntoinfty}dfrac{sqrt[n]{5^n}}{sqrt[n]{n^4}}=limlimits_{ntoinfty}dfrac{5}{1}=5>1$

А значит ряд расходится по признаку Коши

Answer 2

там либо коши либо даламбер