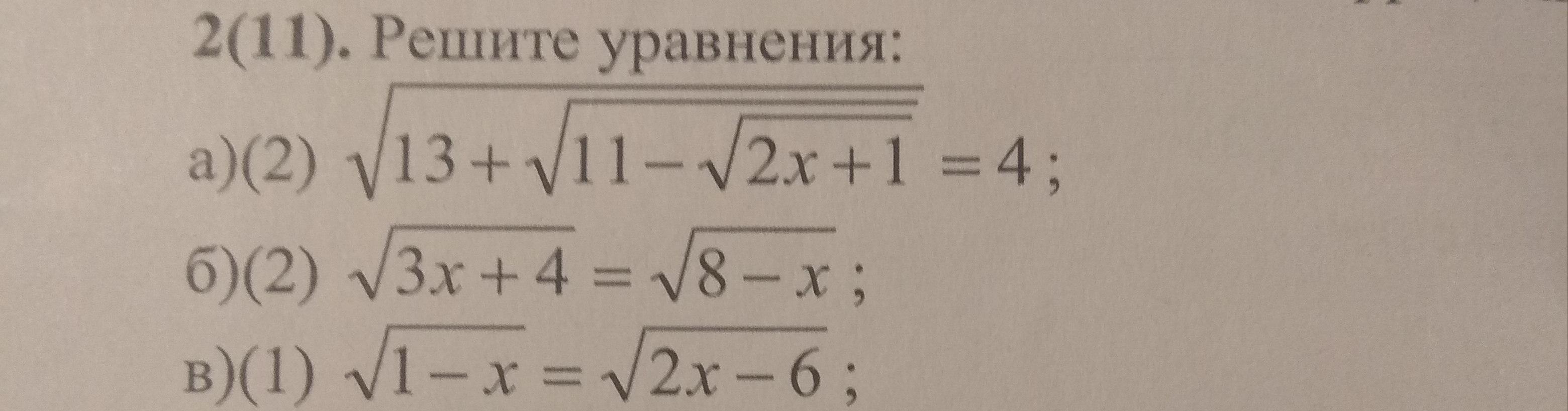Ответы
Ответ дал:
0
ОТВЕТ: 1)1,5; 2)1; 3) нет корней.
Ответ дал:
0
в 3 примере неверно ОДЗ
Ответ дал:
0
1)
2)
3)
=> Нет корней
Ответ дал:
0
Поможешь ещё, пожалуйста?
Вас заинтересует
2 года назад
3 года назад
9 лет назад
9 лет назад