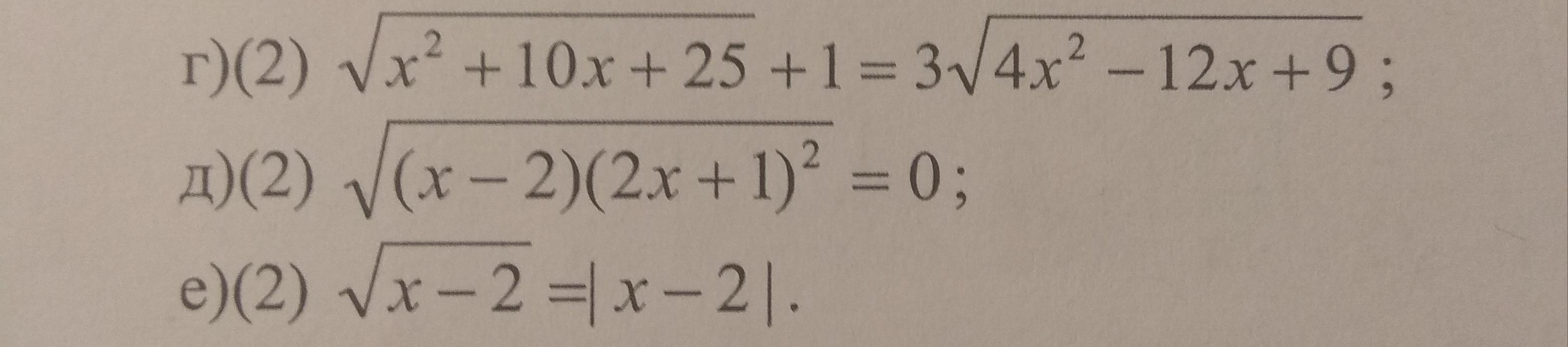Question

Решите уравнения с корнями:

Answer 1

Объяснение:

$1) sqrt{x^2+10x+25}+1=3sqrt{4x^2-12x+9}\sqrt{(x+5)^2}+1=3sqrt{(2x-3)^2} \|x+5|+1=3|2x-3|$

Рассматриваем следующие случаи:

1) Если x ≥1,5, то имеем уравнение

$x+5+1=3(2x-3)\x+6=6x-9\6x-x=6+9\5x=15\x=3$

2) если -5 < x < 1,5,то имеем уравнение

$x+5+1=-3(2x-3)\x+6=-6x+9\x+6x=9-6\7x=3\x=frac{3}{7}$

3) если x ≤ -5, то имеем уравнение

$-x-5+1=-3(2x-3)\-x-4=-6x+9\-x+5x=9+4\4x=13$

Корень не  ≤ -5, поэтому корнем уравнения он не является.

ОТВЕТ: 3, 3/7.

$2) sqrt{(x-2)(2x+1)^2}=0\left [ {{x-2=0} atop {2x+1=0}} right. left [ {{x=2} atop {x=-0,5}} right.\OTVET: -0,5; 2$

$3) sqrt{x-2}=|x-2|\ left { {{x-2geq 0} atop {x-2=(x-2)^2}} right. left { {{xgeq 2} atop {x-2=x^2-4x+4=0}} right. left { {{xgeq2 } atop {x^2-5x+6=0}} right.(1)\(1)x^2-5x+6=0,\left { {{x_1+x_2=5} atop {x_1x_2=6}} right.Rightarrow x_1=2, x_2=3.\OTVET: 2; 3.$

Answer 2

Спасибо. Поможешь с остальными заданиями?

Answer 3

??