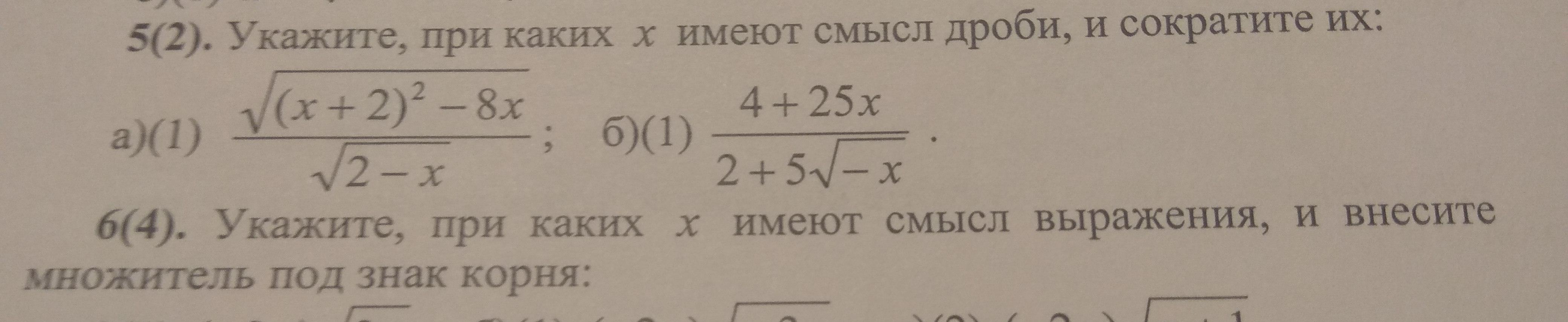Question

Укажите, при каких х имеют смысл дроби, и сократите их:

Answer 1

Объяснение:

$1) frac{sqrt{(x+2)^2-8x} }{sqrt{2-x} }=frac{sqrt{x^2+4x+4-8x} }{sqrt{2-x}}=frac{sqrt{x^2-4x+4} }{sqrt{-(x-2)}}=frac{sqrt{(x-2)^2}}{sqrt{-(x-2)}}=sqrt{frac{(x-2)^2}{-(x-2)} }=sqrt{-(x-2)}=sqrt{2-x}.$

Дробь имеет смысл в том случае, когда 2 - x > 0 (поскольку числитель неотрицателен, то корень в числителе имеем смысл всегда, а знаменатель требует два условия: 1) под корнем должно быть неотрицательное число, 2) знаменатель не должен быть равен 0).  Из неравенства получаем, что x < 2 - только при таких значениях х дробь имеет смысл.

2) Дробь имеем смысл в том случае, когда -x ≥ 0 ⇒ x ≤ 0. Условие того, что знаменатель не должен равняться 0, требовать необязательно, поскольку нет таких значений х, при которых знаменатель обнуляется. Итого дробь имеем смысл при всех x ≤ 0.

Упрощать выражение будем следующим образом: и числитель, и знаменатель домножаем на сопряженное знаменателю выражение 2 - 5√-х:

$frac{4+25x}{2+5sqrt{-x}}=frac{(4+25x)(2-5sqrt{-x}}{(2+5sqrt{-x})(2-5sqrt{-x})} =frac{(4+25x)(2-5sqrt{-x})}{2^2-(5sqrt{-x})^2} =frac{(4+25x)(2-5sqrt{-x})}{4-25cdot(-x)}=frac{(4+25x)(2-5sqrt{-x})}{4+25x}=2-5sqrt{-x}.$

Answer 2

$1); ; y=frac{sqrt{(x+2)^2-8x}}{sqrt{2-x}}\\OOF:; left { {{2-xgeq 0; ,} atop {2-xne 0}} right.; ; to ; ; 2-x>0; ,; ; boxed {x<2}\\frac{sqrt{(x+2)^2-8x}}{sqrt{2-x}}=sqrt{frac{x^2+4x+4-8x}{2-x}}=sqrt{frac{4-4x+x^2}{2-x}}=sqrt{frac{(2-x)^2}{2-x}}=sqrt{2-x}$

$2); ; y=frac{4+25x}{2+5sqrt{-x}}\\OOF:; ; left { {{2+5sqrt{-x}ne 0; ,} atop {-xgeq 0qquad ; ; }} right.; ; to ; ; -xgeq 0; ; ,; ; boxed {xleq 0}\\\frac{4+25x}{2+5sqrt{-x}}=frac{(4+25x)(2-5sqrt{-x})}{(2+5sqrt{-x})(2-5sqrt{-x})}=frac{(4+25x)(2-5sqrt{-x})}{4-5^2(sqrt{-x})^2}=frac{(4+25x)(2-5sqrt{-x})}{4-25cdot (-x)}=\\=frac{(4+25x)(2-5sqrt{-x})}{4+25x}=2-5sqrt{-x}$