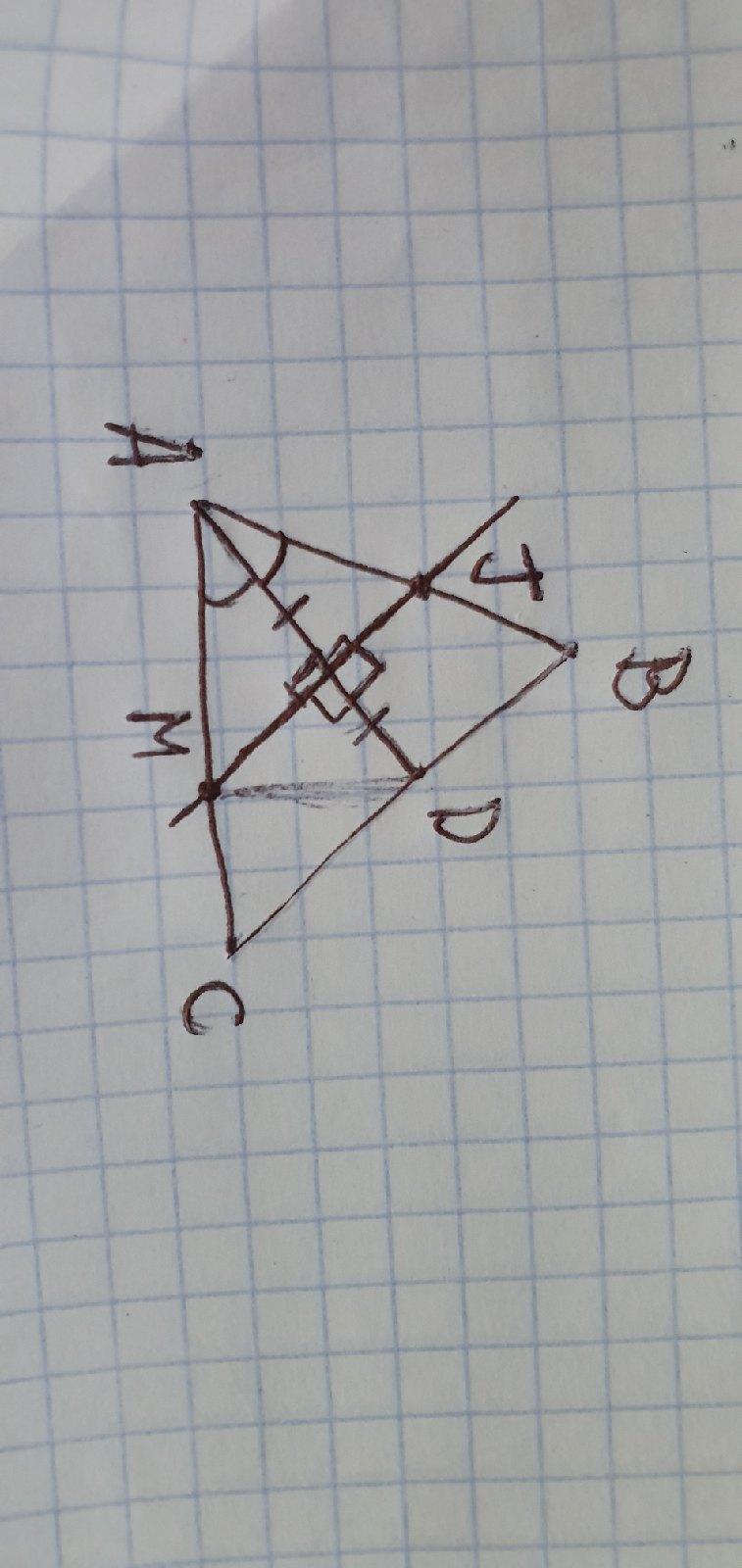Прямая, проходящая через середину биссектрисы AD треугольника ABC и перпендикулярная к AD, пересекает сторону AC в точке M. Докажите что MD параллельна AB
Ответы
Объяснение:
Нарисовал я конечно так себе, но это почти не влияет на решение(Там еще в центре точка О, забыл пометить).
Рассмотрим треугольники AOJ и AOM:
1. JAO = MAO(так как AD - биссектриса),
2. AO - общая сторона,
3. AOJ = MOA = 90°,
Следовательно, треугольники AOJ и AOM равны по стороне и двум прилежащих к ней углам.
Значит, стороны JO и MO - равны, как соответственные стороны равных треугольников.
Рассмотрим треугольники MOD и JOA:
1. JOA = MOD(по условию),
2. AO = OD(по условию)
3. JO = MO(как было сказано ранее)
Следовательно, треугольники равны по двум сторонам и углу между ними.
Значит, углы OMD и OJA - равны, как соответственные углы равных треугольников.
Углы OMD и OJA - накрест лежащие при прямых AB и MD и секущей JM. Следовательно, AB || MD, ч. т. д.