Question

Найдите стороны параллелограмма ABCD если его диагональ BD равна 10 см делит угол B на части в 48 и 72 градуса​

Answer 1

Ответ:

Стороны параллелограмма равны ≈8,6см; ≈8,6см; ≈11см; ≈11см.

Объяснение:

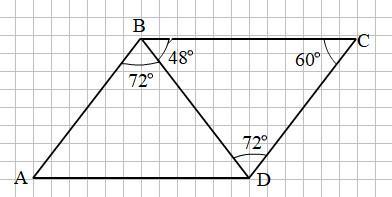
Смотри прикреплённый рисунок.

Пусть ΔABD = 72°, a  ∠CBD = 48°

∠CDB = ∠ABD = 72° (накрест лежащие углы при AB || CD и секущей BD)

В ΔBCD по свойству углов треугольника ∠BCD = 180° - (48° + 72°) = 60°

По теореме синусов в ΔBCD получим следующие отношения:

$frac{BD}{sin60^circ }= frac{CD}{sin48^circ } =frac{BC}{sin72^circ }$

Из соотношения

$frac{BD}{sin60^circ }= frac{CD}{sin48^circ }$

найдём меньшую сторону CD параллелограмма

$CD = BDcdot frac{sin48^circ}{sin60^circ} = 10cdot frac{0.7431}{0.866}=8. 581 (cm)$

Из соотношения

$frac{BD}{sin60^circ }=frac{BC}{sin72^circ }$

найдём большую сторону ВC параллелограмма

$BC = BDcdot frac{sin72^circ}{sin60^circ} = 10cdot frac{0.851}{0.866}=10.981 (cm)$