Question

30 баллов! периметр ромба равен 36, а один из его углов 60°. Найдите площадь ромба​

Answer 1

Объяснение:

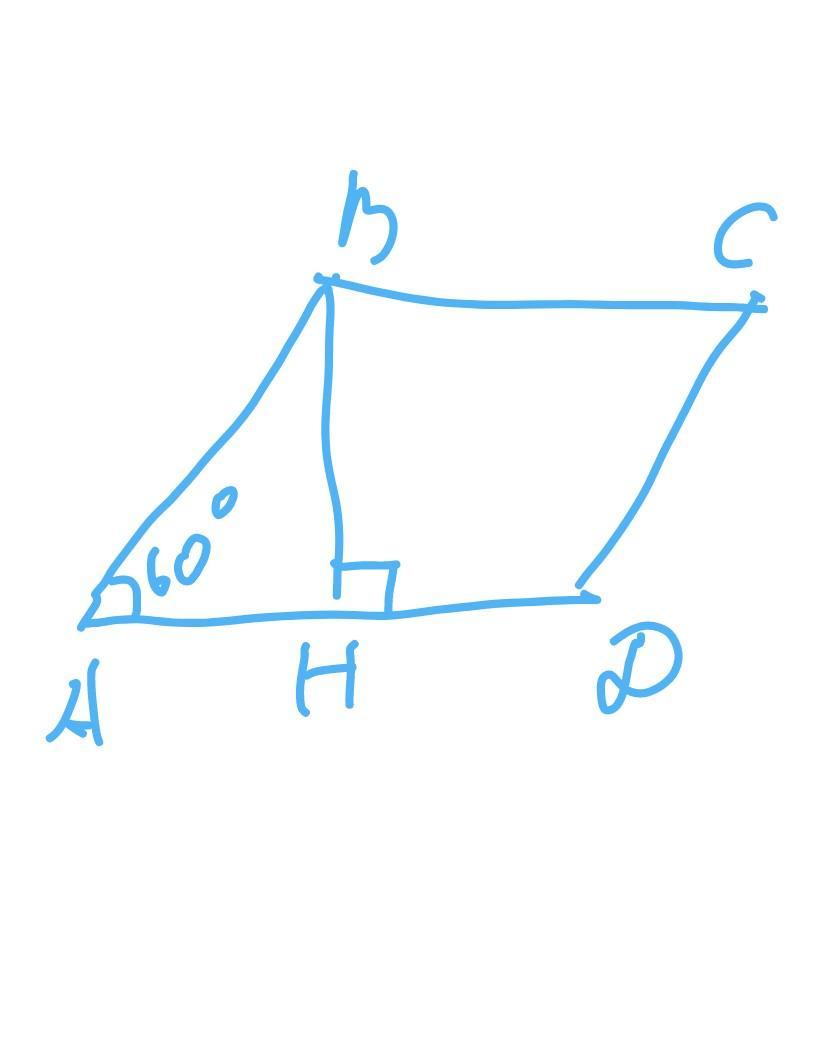
сторона ромбы равна периметру Р/4=36/4=9

проведем высоту BH, при условии, что угол А=60 градусов., тогда угол ABH=30 градусам. А напротив угла 30 градусов лежит катет, равный половине гипотинузы. AH=AB/2=9/2=4,5

по теореме пифагора

$bh = sqrt{ {ab}^{2} - {ah}^{2} } = sqrt{ {9}^{2} - { frac{9}{2} }^{2} } = sqrt{ {9}^{2}(1 - frac{1}{4} ) } = 9 sqrt{0.75}$

площадь ромба равна S=AD×BH=9×9 корень 0.75=81 корень из 0.75