Question

Sin^2 (2x) +2 sin (x) - 3=0

Answer 1

$sin^{2} 2x + 2sin x - 3 = 0\4sin^{2} x cos^{2} x + 2sin x - 3 = 0\4sin^{2} x (1 - sin^{2}x) + 2sin x - 3 = 0\4sin^{2} x -4sin^{4} x + 2sin x - 3 = 0$

Замена: $sin x = t, t in [-1; 1]$

$4t^{2} - 4t^{4} + 2t - 3 = 0$

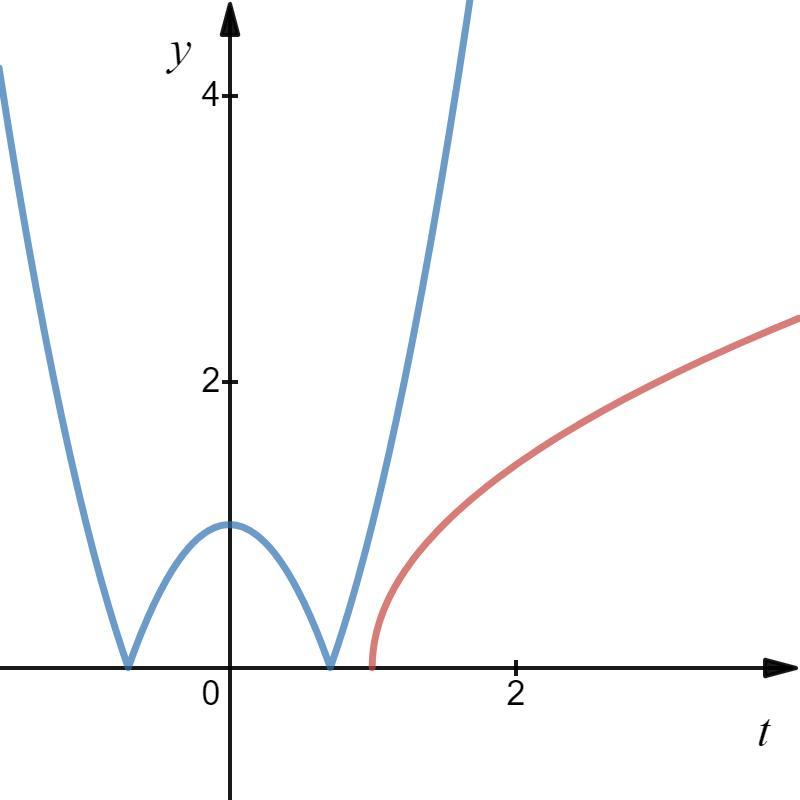
Решим уравнение графически, для этого преобразуем его.

$2t - 3 = 4t^{4} - 4t^{2}\2t - 3 + 1 = 4t^{4} - 4t^{2} + 1\2t - 2 = (2t^{2} - 1)^{2}\sqrt{2t - 2} = sqrt{(2t^{2} - 1)^{2}}\sqrt{2t - 2} =|2t^{2} - 1|$

Рассмотрим две функции: $y = sqrt{2t -2}$ и $y = |2t^{2} - 1|$. Изобразим их на координатной плоскости (см. вложение). Видим, что нет точек пересечения. Делаем вывод: заданное уравнение не имеет действительных корней.

Ответ: нет действительных корней.