Помогите!( Не пишите ответ пожалуйста кто не знает, не надо мне решать через Photomath)
Решите уравнение 2 sin 2 x + 2 t g 2 x + 4 t g x − 2 (√ 2 )sin x + 3 = 0
Приложения:
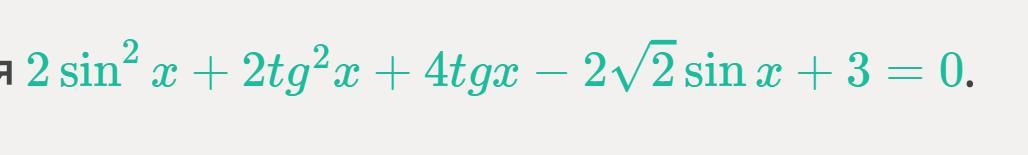
Ответы
Ответ дал:
0
2(tg^2(x)+2tg(x)+1)=2(tg(x)+1)^2
2sin^2(x)-2√2*sin(x)+1=(√2*sin(x)-1)^2
тогда уравнение сводится к виду
2(tg(x)+1)^2+(√2*sin(x)-1)^2=0
так как слева положительные слагаемые, то их сумма равна 0, когда каждый из них 0
тогда получаю систему 2 уравнений
tg(x)+1=0; √2*sin(x)-1=0;
tg(x)=-1; x=3pi/4+pik
√2*sin(x)-1=0; sin(x)=1/√2=√2/2; x=pi/4+2pik и x=3pi/4+2pik
оба уравнения равны 0 одновременно при общем корне
x=3pi/4+2pik
Вас заинтересует
2 года назад
3 года назад
3 года назад
8 лет назад
9 лет назад