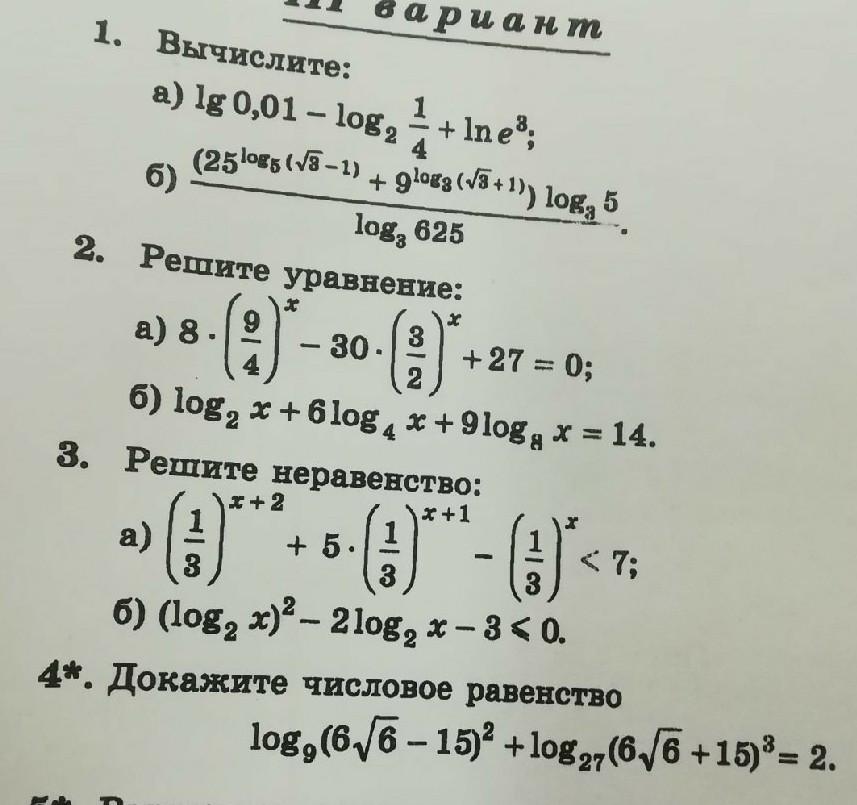Question

Ребят,помогите пожалуйста решить 4 номера, очень надо, ничего не понимаю​

Answer 1

Ответ:

Объяснение:

прикрепляю во вложении

Answer 2

сейчас исправлю ответ

Answer 3

Я из Харькова.

Answer 4

Извините, перепутала вас с моим знакомым. Ник похожий

Answer 5

4. Докажите числовое равенство $log_{9}(6sqrt{6} - 15)^{2} + log_{27}(6sqrt{6} + 15)^{3} = 2.$

Доказательство.

Применим следующие свойства логарифмов:

$1) log_{a}b^{k} = klog_{a}b \2) log_{a^{k}}b = dfrac{1}{k}log_{a}b \3) log_{a}b + log_{a}c = log_{a}(bc)\4^{*}) log_{a}b^{2n} = 2nlog_{a}|b|, n in Z$

Получаем:

$log_{9}(6sqrt{6} - 15)^{2} + log_{27}(6sqrt{6} + 15)^{3} = 2log_{3^{2}}|6sqrt{6} - 15| + 3log_{3^{3}}(6sqrt{6} + 15) =\= 2 cdot dfrac{1}{2} log_{3}(15 - 6sqrt{6}) + 3 cdot dfrac{1}{3} log_{3}(6sqrt{6} + 15) = log_{3}(15 - 6sqrt{6})+log_{3}(6sqrt{6} + 15)=\= log_{3}left[(15 - 6sqrt{6})(6sqrt{6} + 15) right] = log_{3}(15^{2} - 36 cdot 6) = log_{3}9 = 2$

Числовое равенство доказано.