Question

знайдіть висоту трапеції, бічні сторони якої становлять 10 і 17 а основи дорівнюють 20 і 41

Answer 1

Дано:

ABCD-трапеция

AB=10

CD=17

BC=20

AD=41

Найти: BH

Решение:

Проведем BM║CD, тогда MBCD-параллелограмм(т.к. BM║CD и BC║MD).

Если MBCD-параллелограмм, то CD=BM=17 и BC=MD=20.

AM=AD-MD=41-20=21.

$displaystyle S_{triangle}=sqrt{p(p-a)(p-b)(p-c)}$ - формула Герона, где p-полупериметр, a,b,c - стороны треугольника. Найдем площадь ΔABM:

$displaystyle p=frac{AB+BM+AM}{2}=frac{10+17+21}{2} =24 \S_{triangle ABM}=sqrt{24(24-10)(24-17)(24-21)} =sqrt{24cdot 14cdot 7cdot 3} =84$

Найдем высоту BH:

$displaystyle S_{triangle ABM}=frac{1}{2}cdot BHcdot AM;;Rightarrow;;BH=frac{2S_{triangle ABM}}{AM} =frac{2cdot 84}{21} =8$

Ответ: BH=8.

Answer 2

https://geleot.ru/education/math/geometry/height/trapezoid

Answer 3

Оки, спасибо и на этом)

Answer 4

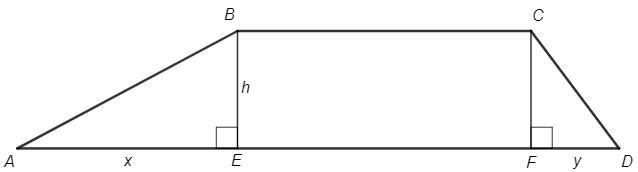
Трапеция, BC - меньшее основание.

Опустим высоты BE и CF

AE=x, DF=y

x+y=AD-BC =21 (EF=BC тк EBCF прямоугольник)

По теореме Пифагора

ABE: x^2 +h^2 =17^2

DCF: y^2 +h^2 =10^2

x^2 -y^2 =17^2 -10^2 =189

(x-y)(x+y) =189

x-y =189/21 =9

2x=30 => x=15

h=√(17^2-15^2) =8