Question

Найдите площадь закрашенных фигур. Нужны задачи 2,6,3,7,8,4

Answer 1

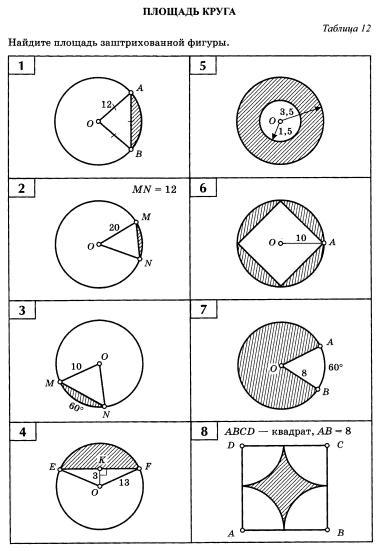
2. Проведём в ΔOMN высоту OH. Тогда HM = 6 (OH -- медиана)

$OH=sqrt{OM^2-MH^2}=sqrt{400-36}=sqrt{364}=2sqrt{91}$

$S_{Delta OMN}=frac{1}{2}MNcdot OH=12sqrt{91}\ \ S_{Delta OMN}=frac{1}{2}OMcdot OHcdot sinangle O=200sinangle O=12sqrt{91} \ \ sinangle O=0,06sqrt{91}\ \ angle O=arcsin(0,06sqrt{91})$

$S_{cekm.}=pi R^2cdotfrac{alpha}{360^{circ}}\ \ S_{cekm.}=pi cdot20^2cdotfrac{arcsin(0,06sqrt{91})}{360}=frac{10pi}{9}cdot arcsin (0,06sqrt{91})\ \ \ S_{uck.}=S_{cekm.}-S_{Delta OMN}=frac{10pi}{9}cdot arcsin (0,06sqrt{91})-12sqrt{91} \ \ OTBET:frac{10pi}{9}cdot arcsin (0,06sqrt{91})-12sqrt{91}$

3. ∠MON опирается на дугу MN -- центральный угол ⇒ ∠MON = 60°

$S_{Delta OMN}=frac{1}{2}cdot MO cdot ONcdot sinangle O=frac{1}{2}cdot 10 cdot 10cdot sin60^{circ}=50cdotfrac{sqrt{3}}{2}=25sqrt{3}$

$S_{cekm.}=pi cdot10^2cdotfrac{60}{360}=frac{50pi}{3} \ \ \ S_{uck.}=S_{cekm.}-S_{Delta OMN}=frac{50pi}{3}-25sqrt{3} \ \ OTBET:frac{50pi}{3}-25sqrt{3}$

4. Так как ΔOFE -- р/б, то OK -- медиана ⇒ EK = KF

$EF=2KF=2sqrt{OF^2-OK^2}=2sqrt{169-9}=2sqrt{160}=8sqrt{10}$

$S_{Delta OFE}=frac{1}{2}OKcdot EF=frac{1}{2} cdot 3 cdot8sqrt{10}=12sqrt{10} \ \ S_{Delta OFE}=frac{1}{2}OEcdot OFcdot sinangle O=frac{169}{2}cdot sinangle O=12sqrt{10} \ \ sinangle O=frac{24sqrt{10} }{169} \ \ angle O=arcsin(frac{24sqrt{10} }{169} )$

$S_{cekm.}=pi cdot13^2cdotfrac{arcsin(frac{24sqrt{10} }{169} )}{360}=frac{169pi}{360}cdot arcsin (frac{24sqrt{10} }{169})\ \ \ S_{uck.}=S_{cekm.}-S_{Delta OFE}=frac{169pi}{360}cdot arcsin (frac{24sqrt{10} }{169})-12sqrt{10} \ \ OTBET:frac{169pi}{360}cdot arcsin (frac{24sqrt{10} }{169})-12sqrt{10}$

6. Площадь закрашенной фигуры можно получить, если из круга "вырезать" белый квадрат.

$S_{kp.}=pi R^2=picdot 10^2=100pi$

Пусть a -- сторона квадрата. Если из точки O провести радиус к соседней вершине квадрата, то получится треугольник, из которого

$a=sqrt{10^2+10^2}=sqrt{200}=10sqrt{2}\ \ S_{k.}=a^2=200\ \ \ S_{uck.}=S_{kp.}-S_{k.}=100pi-200\ \ OTBET:100pi-200$

7. ∠AOB малый опирается на дугу AB -- центральный угол ⇒ ∠AOB малый = 60°. Найдём больший угол AOB.

$angle AOB=360^{circ}-60^{circ}=300^{circ}\ \ \ S_{uck.}=pi cdot8^2cdotfrac{300}{360}=frac{160pi}{3} \ \ OTBET:frac{160pi}{3}$

8. Каждая белая часть -- это четверть круга. Вместе они образуют круг с радиусом в половину стороны квадрата.

$S^*_{kp.}=pi R^2=pi cdot(frac{AB}{2})^2=picdot4^2=16pi\ \ S_{k.}=AB^2=64\ \ \ S_{uck.}=S_{k.}-S^*_{kp.}=64-16pi\ \ OTBET:64-16pi$