Question

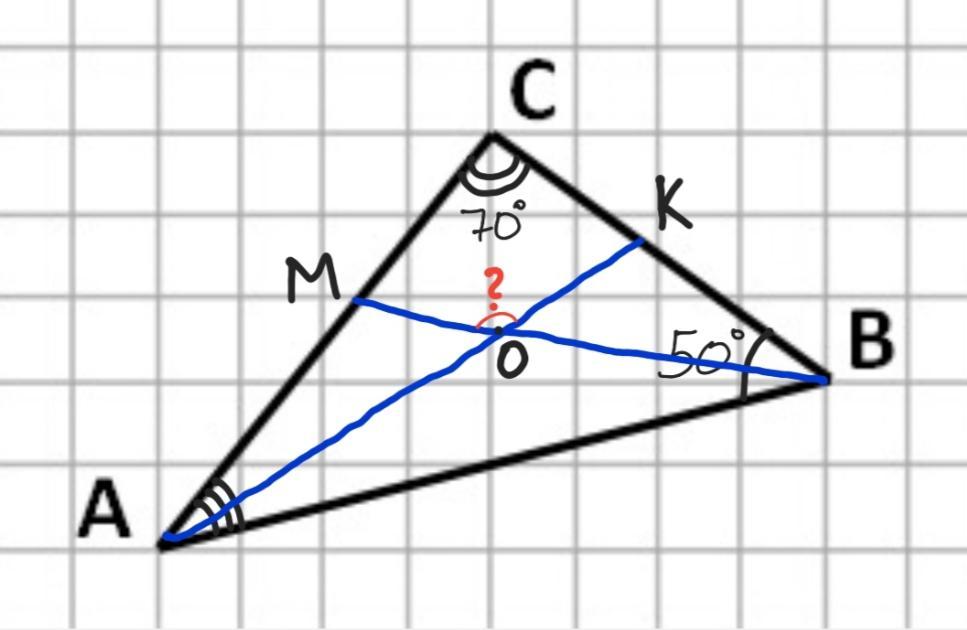
4. В треугольнике
ABC уголB = 50°, уголC=70°. Биссектрисы АК
и BM треугольника ABC пересекаются в точке 0. Найди-
те угол КОМ.​

Answer 1

Решение.

Найдём третий угол треугольника АВС.

∠А= 180°-∠В - ∠С= 180°-50°-70°=60°(поскольку сумма всех углов треугольника равна 180°).

Так как АК и ВМ - биссектрисы ΔABC, то углы САК и ВАК равны, а также равны между собой углы СВМ и АВМ.

∠ВАК=∠А : 2= 60° : 2 = 30°.

∠АВМ=∠В : 2 = 50° : 2 = 25°.

В ΔAOB: поскольку сумма всех углов равна 180°, то

∠АОВ = 180°-∠ВАО-∠АВМ= 180°-30°-25°= 125°.

∠КОМ =∠АОВ как вертикальные, поэтому ∠КОМ=125°.

ОТВЕТ: 125°