Question

Найдите площадь робма сторона которого 50 см а разности диагоналей 20 см.
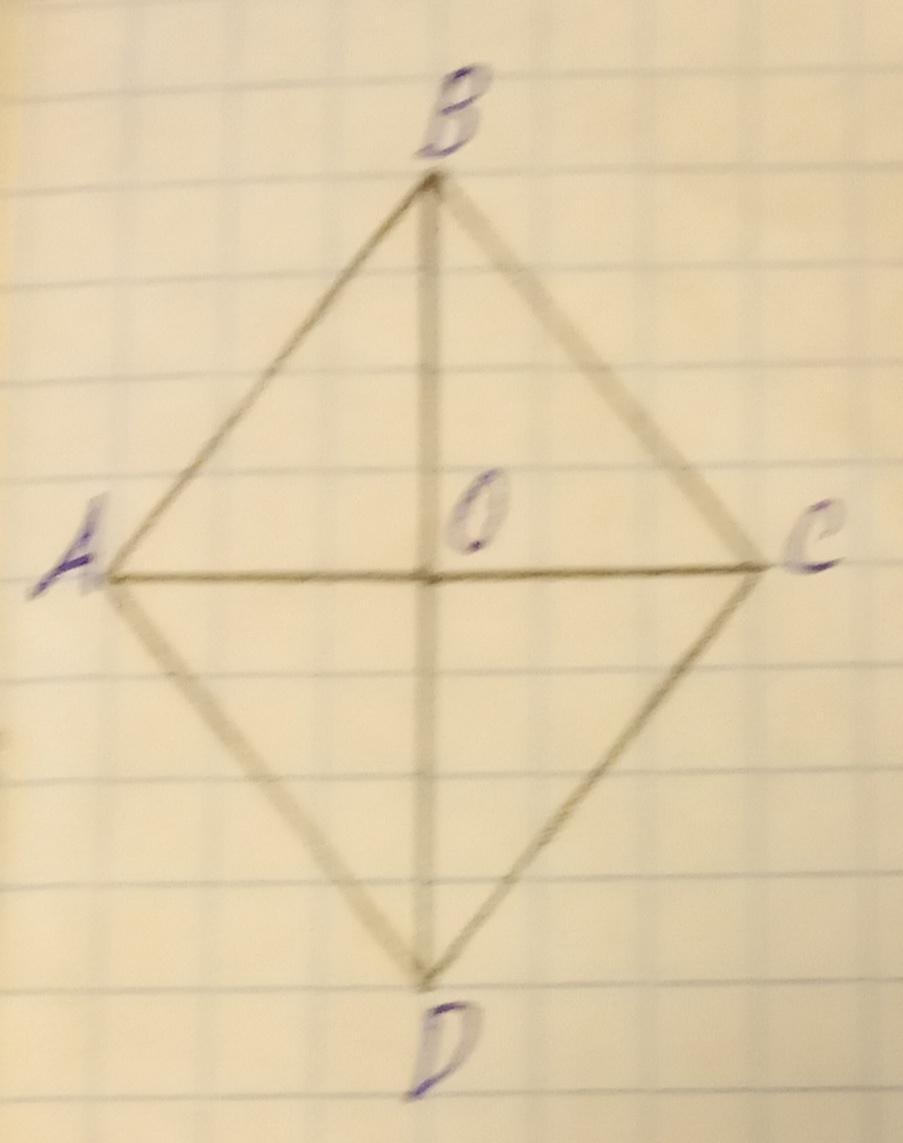
Дано: АВСD — ромб, AB = 50 см, ВD больше АС на 20 см.
Найти: S ромба.
Решение: Пусть АО — x см, тогда АС — 2х см, тк. О — точка пересечения диагоналей. ВD – AC = 20 см, значит ВD = AC +20 см, следовательно ВD = (2x +20), а ВО = (x + 10). Треугольник AOB — прямоугольный, поскольку диагонали ромба перпендикулярны по теореме, значит АО² + ВО² = АВ², следовательно х² + (x+10)²= 50² по теореме Пифагора.
2х² + 20х + 100 = 2500 (по формуле сокращённого умножения)
2x² + 20x = 2500 – 100
2x² + 20x = 2400
Помогите пожалуйста! Я почти уже решила, но не знаю, что делать дальше. ПОДРОБНО ПОЖАЛУЙСТА!

Answer 1

Ответ:

...................................