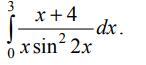Question

Выяснить сходимость несобственного интеграла

Answer 1

$xsin^22x=0=>x=0;;;;sin2x=0\ left;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;x=frac{pi n}{2}$

Значит особые точки $0; dfrac{pi}{2}$

$limlimits_{xto0}dfrac{x+4}{xsin^22x}=limlimits_{xto0}dfrac{x+4}{xcdot(2x)^2}=limlimits_{xto0}dfrac{x+4}{4x^3}=infty$

$f(x)=dfrac{x+4}{xsin^22x}\ int limits_0^3f(x)dx= int limits_0^1f(x)dx+ int limits_1^{frac{pi}{2}}f(x)dx+ int limits_frac{pi}{2}^3f(x)dx$

$f(x)geq 0;forall;xin[0;3]$, а значит если хотя бы один из интегралов в сумме расходится, то и исходный интеграл расходится.

$f(x)limits_{xto 0}sim dfrac{4}{xcdot (2x)^2}=dfrac{1}{x^3}=dfrac{1}{(x-0)^3}\ 3>1$

А значит $intlimits_0^1f(x)dx$ расходится по степенному признаку.

А значит и исходный интеграл расходится

Answer 2

Спасибо огромное!!!!!!!!!!!!!