Если угол одного из прямоугольных треугольников равен 30 °, докажите, что катет расположенный в противоположном углу равен половине гипотенуза.
Ответы
Ответ дал:
0
Ответ:
Пусть АВС - прямоугольный треугольник, у которого ∠С=90 градусов, а ∠А=30 градусов. А тогда по теореме о сумме углов треугольника ∠В=60 градусов. Докажем, что катет ВС равен половине гипотенузы АВ.
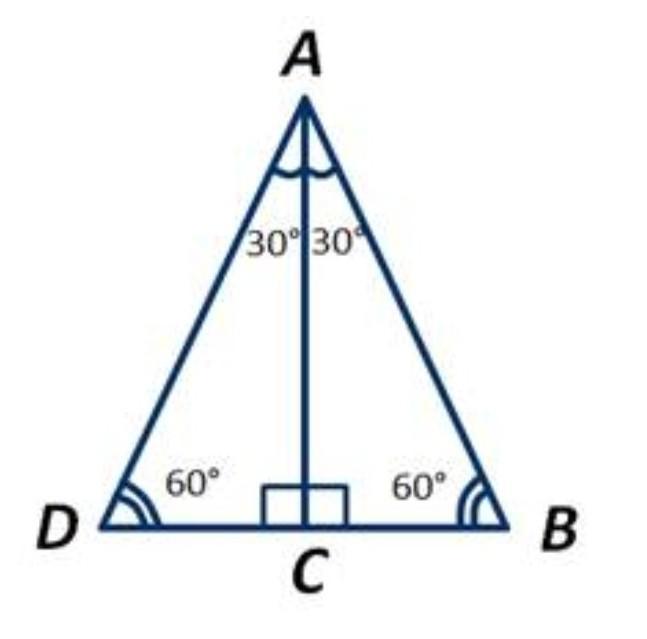
Приложим к треугольнику АВС равный ему треугольник АСD следующим образом (рисунок)
Получили, что у треугольника АВD все углы равны по 60 градусов, то есть он является равносторонним.
Получим:
BC= 1/2 BD . А т.к. АВD равносторонний AB=BD следовательно
ВС= 1/2 АВ.
ч.т.д.
Приложения:
Вас заинтересует
2 года назад
3 года назад
3 года назад
9 лет назад
9 лет назад
10 лет назад