Question

як знайти кількість цілих розв'язків нерівності, опишіть, як ви зробили завдання

3x^2 + 5x - 8 < 0

Answer 1

$3x^{2} + 5x - 8 < 0$

Маємо відповісти на запитання: при яких значеннях змінної $x$ графік функції (парабола) $y = 3x^{2} + 5x - 8$ знаходиться під віссю абсцис (на від'ємних ординатах).

Знайдемо точки перетину цієї параболи з віссю абсцис. Для цього прирівняємо функцію до нуля:

$3x^{2} + 5x - 8 = 0\a = 3; b = 5; c = -8\D = b^{2} - 4ac = 5^{2} - 4cdot 3 cdot (-8) = 25 + 96 = 121$

$x_{1,2} = dfrac{-b pm sqrt{D}}{2a} = dfrac{-5 pm 11}{6} = left[begin{array}{ccc}x_{1} = 1 \x_{2} = -2dfrac{2}{3} \end{array}right$

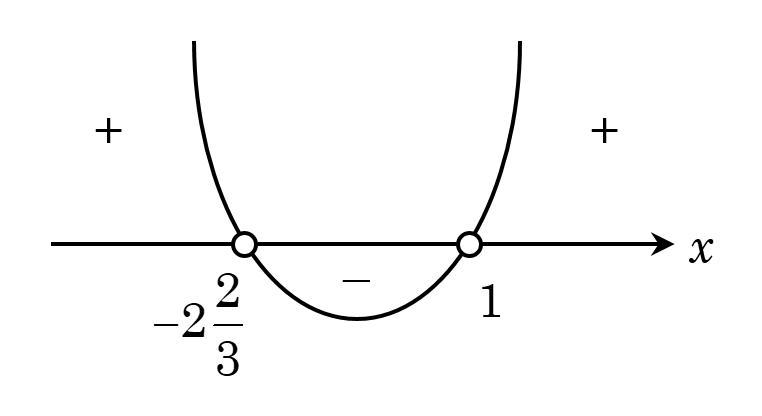
Намалюємо ескіз цієї параболи з виколотими точками, абсциси яких дорівнюють нулям функції (см. рисунок).

Отже, з рисунка бачимо, що парабола меньше нуля на проміжку $x in left(-2dfrac{2}{3} ; 1 right)$

Тоді цілими розв'язками нерівності будуть $x = {-2; -1; 0 }$

Відповідь: 3 цілих розв'язки.

Answer 2

в задании идёт речь о целых решениях...

Answer 3

А звідки числа - 1; 0??

Answer 4

Ответ:

как-то так

Объяснение: