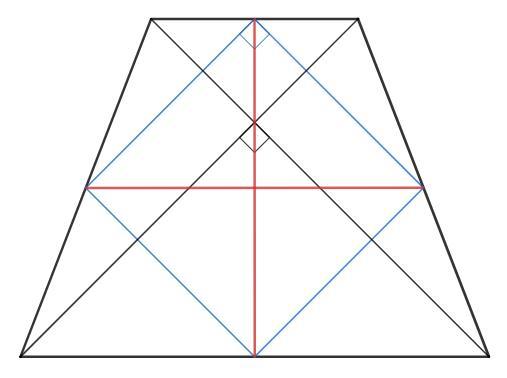
Докажите, что площадь равнобедренной трапеции, диагонали которой пересекаются под прямым углом, равна квадрату его высоты.
Ответы
Каждая задача на доказательство имеет несколько решений.
Вот пара легчайших способов решения данной задачи.


Площадь трапеции равна произведению высоты и средней линии. Докажем, что в равнобедренной трапеции с перпендикулярными диагоналями высота и средняя линия равны.
Соединим середины сторон трапеции. Стороны полученного (синего) четырехугольника параллельны диагоналям трапеции (т.к. являются средними линиями в треугольниках, отсекаемых диагоналями). Отсюда же следует, что угол синего четырехугольника равен углу между диагоналями. Параллелограмм с прямым углом - прямоугольник, его диагонали равны.
В равнобедренной трапеции отрезок, соединяющий середины оснований, является высотой (равнобедренная трапеция - усеченный равнобедренный треугольник, в котором медиана является высотой). Таким образом, высота и средняя линия данной трапеции равны как диагонали прямоугольника.
m=h => S=mh=h^2