Question

ДАЮ МНОГО БАЛЛОВ!!!!
СРОЧНО!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!

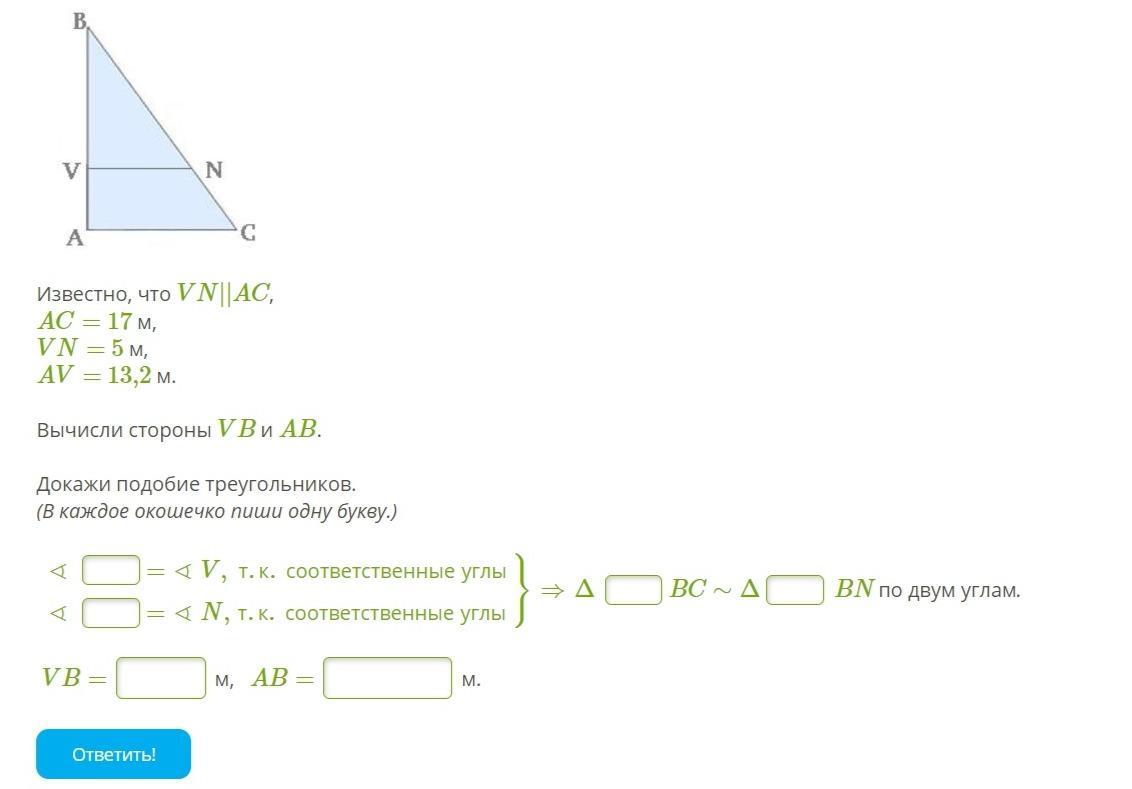
Известно, что VN||AC, AC= 17 м, VN= 5 м, AV= 13,2 м. Вычисли стороны VB и AB. Докажи подобие треугольников. (В каждое окошечко пиши одну букву.)

Сейчас прикреплю фото

Answer 1

Ответ:

<V=<А

<N=<C

следоавтельно треуг.ABC~треуг.BVN

AV=44,88

Answer 2

Ответ:

Объяснение:

Угол BAC = углу BVN как соответственные при VN ║ AC и секущей AB

Угол BCA = углу BNV как соответственные при VN ║ AC и секущей BC

И этого следует,что треугольник BVN подобен треугольнику ABC по двум углам. ⇒ VN/AC = VB/AB. Однако AB = AV + VB = 13,2 + VB;

5/17 = VB/(13,2 + VB)

17 * vb = 5 * (13,2 + vb)

17 * vb - 5*vb = 66

12 * vb = 66

vb = 5,5

Ab = vb + 13,2 = 5,5 + 13,2 = 18,7

Answer 3

Спасибо, сразу не увидел <3