Question

СРОЧНО МНОГО БАЛЛОВ


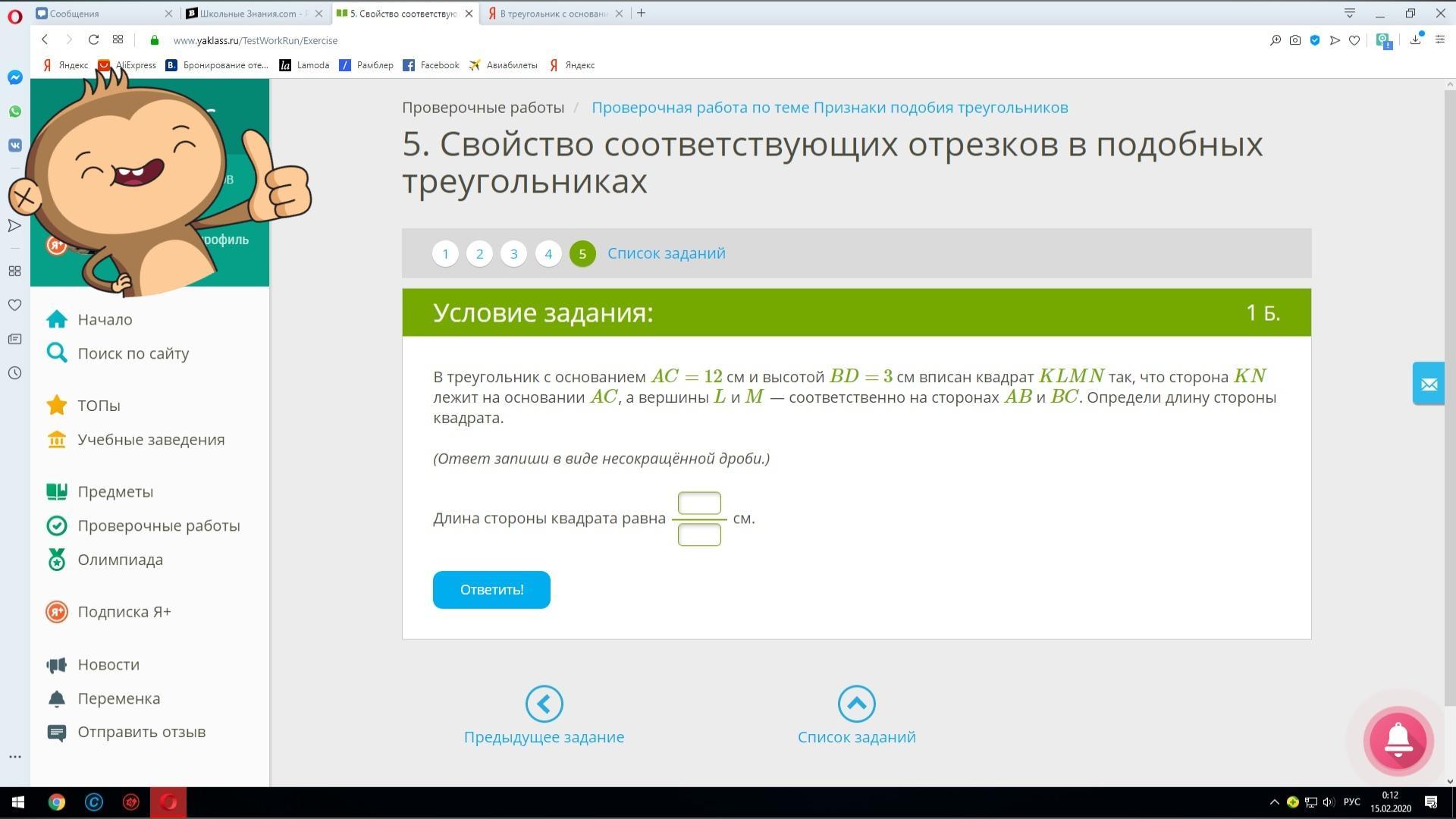
треугольник с основанием AC= 12 см и высотой BD= 3 см вписан квадрат KLMN так, что сторона KN лежит на основании AC, а вершины L и M — соответственно на сторонах AB и BC. Определи длину стороны квадрата. (Ответ запиши в виде несокращённой дроби.) Длина стороны квадрата равна см.

Сейчас прикреплю фото

Answer 1

Ответ:

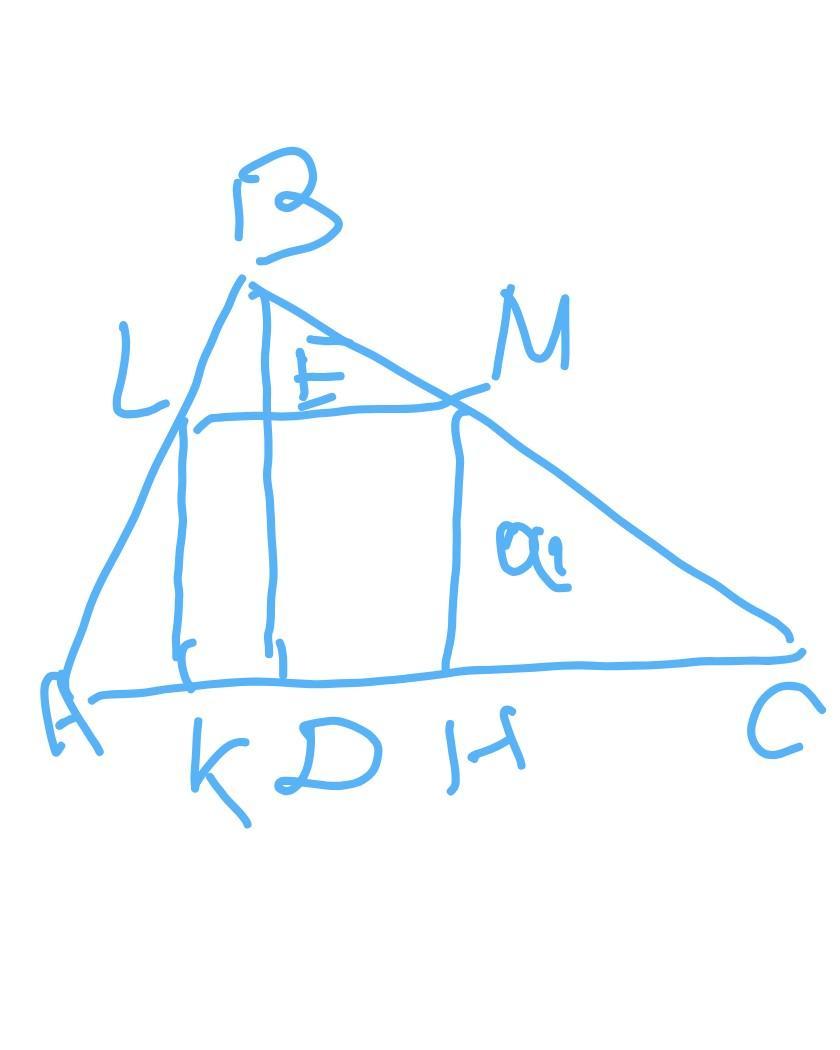
Треугольники ABC и LBM подобны. BD и BE - высоты в них.

Обозначим сторону квадрата через a.

Тогда 

AC/BD=LM/BE=LM/(BD-MN)

Или

16/12=a/(12-a)

откуда a=48/7

Answer 2

Ответ 48/7?

Answer 3

Ответ:

12/5 см

Объяснение:

Пусть сторона квадрата х.

Площадь треугольника 3*12/2=18

Треугольник разбит на 3 треугольника и квадрат.

Площадь верхнего треугольника с вершиной В  х*(3-х)/2

Площадь квадрата: х*х. Сумма площадей оставшихся треугольников

х*(12-х)/2. Составим уравнение

18=х*х+1,5х-0,5х*х+х*6-х*х*0,5

18=7,5х  2,5х=6    х=12/5