Question

Помогите с задачей по геометрии 8 класс
Срочно надо!
Даю 40 балов

Answer 1

Ответ:

42 см²

Объяснение:

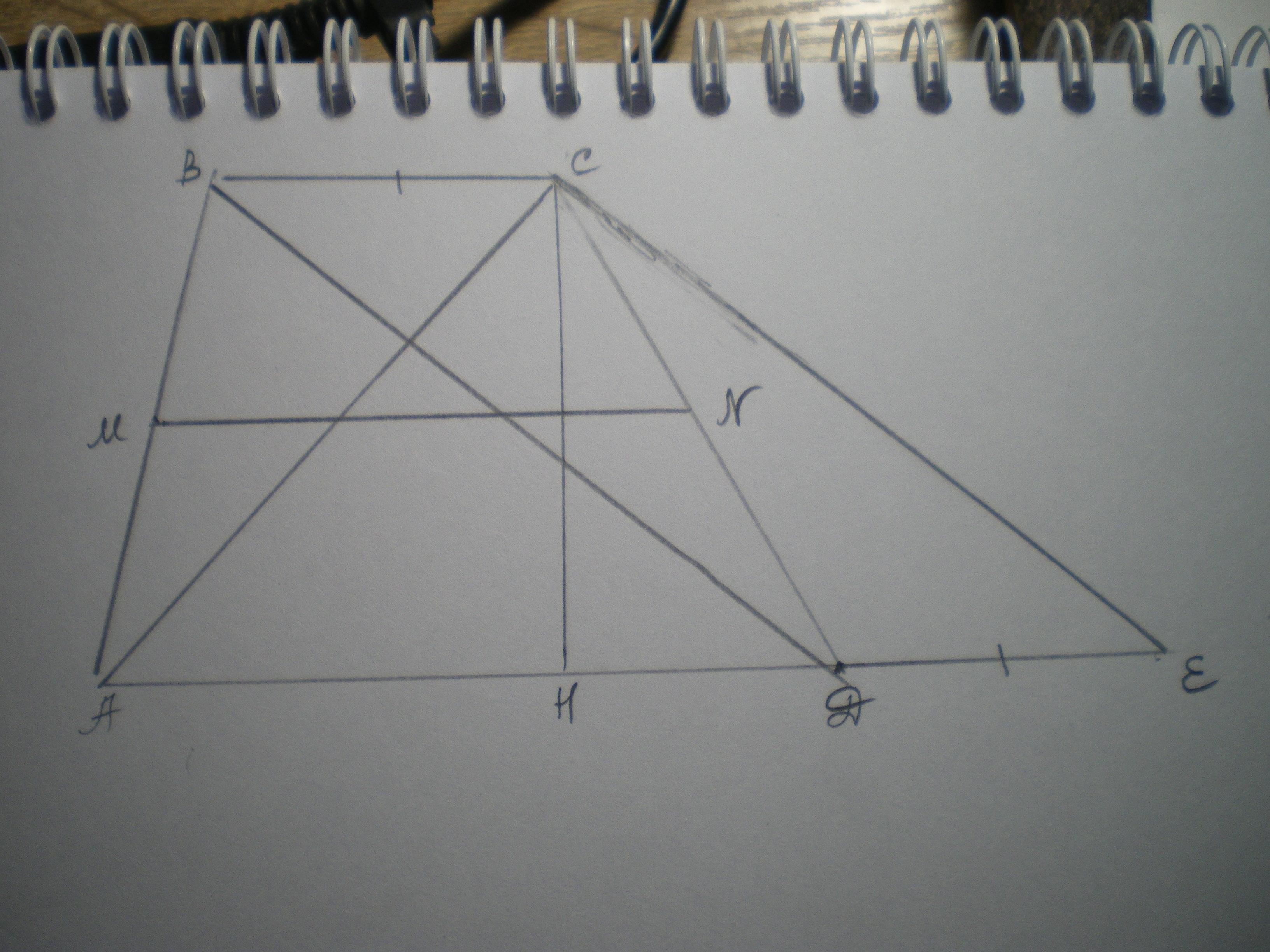
Дано: АВСD - трапеция, АС=7 см, ВD=15 см, МN=10 см. Найти S(ABCD).

Достроим трапецию до параллелограмма, для чего проведем СЕ║ВD и продлим основание АD. По свойству параллелограмма СЕ=ВD=15 cм., а DЕ=ВС.

Поскольку ВС+AD=2MN по свойству средней линии трапеции, то AD+DE=10*2=20 cм;  АЕ=20 см.

Найдем S(АСЕ) по формуле Герона:

p=(AC+CE+AE):2=(7+15+20):2=21 cм

S=√(p(p-a)(p-b)(p-c))=√(21*14*1*6)=√1764=42 см²

Найдем высоту СН через площадь ΔАСЕ

42=(1/2)*20*СН;  42=10СН;  СН=4,2 см.

Найдем S(ABCD)

S(ABCD)=MN*CH=10*4,2=42 см²