Question

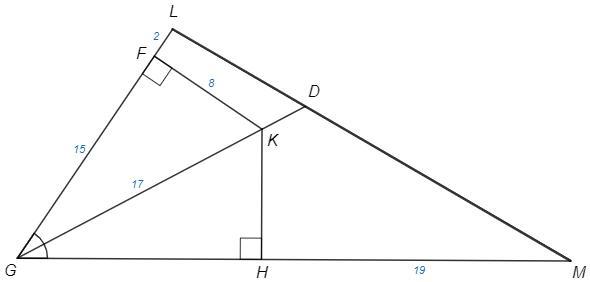
Прямая, проходящая через точки G и K, служит биссектрисой угла FGH. Известно, что KF перпендикулярна GF , KH перпендикулярна GH , KF=KH=8 , GK=17. Отрезок GL содержит точку F, FL=2. Отрезок GM содержит точку H и HM =19. Найдите длину отрезка ML

Answer 1

GF =√(GK^2 -KF^2) =15

sin(G/2) =8/17

cos(G/2) =15/17

cosG =cos(G/2)^2 -sin(G/2)^2 =7*23/17^2

△GKH=△GKF => GH=GF

GL =15+2 =17

GM =15+19 =34

Теорема косинусов

ML^2 =GL^2 +GM^2 -2GL*GM*cosG =17^2 +34^2 -644 =801

ML =√801 =3√89